题目内容
设直线l的方程为(m2-2m-3)x+(2m2+m-1)y=2m-6(m∈R,m≠-1),根据下列条件分别求m的值:
①l在x轴上的截距是-3;
②斜率为1.
①l在x轴上的截距是-3;
②斜率为1.
分析:①l在x轴上的截距是-3,即直线l过点(-3,0),代入方程,解之即可;②由题意得斜率为1,即直线方程中x、y的系数互为相反数,且不为0,解方程求得实数m的值.
解答:解:①l在x轴上的截距是-3,即直线l过点(-3,0),
故(m2-2m-3)(-3)+(2m2+m-1)•0=2m-6,
即3m2-4m-15=0,分解因式的(x-3)(3x+5)=0,
解得m=3或,m=-
,
经检验当m=3时,直线方程为x=0,不合题意,应舍去,
故m=-
;
②直线斜率为1,即直线方程中x、y的系数互为相反数,且不为0.
故(m2-2m-3)+(2m2+m-1)=0,解得m=
,或m=-1
但m=-1时,2m2+m-1=0,故应舍去,
所以m=
故(m2-2m-3)(-3)+(2m2+m-1)•0=2m-6,
即3m2-4m-15=0,分解因式的(x-3)(3x+5)=0,
解得m=3或,m=-
| 5 |
| 3 |
经检验当m=3时,直线方程为x=0,不合题意,应舍去,
故m=-
| 5 |
| 3 |
②直线斜率为1,即直线方程中x、y的系数互为相反数,且不为0.
故(m2-2m-3)+(2m2+m-1)=0,解得m=
| 4 |
| 3 |
但m=-1时,2m2+m-1=0,故应舍去,
所以m=
| 4 |
| 3 |
点评:本题考查直线的倾斜角和斜率的关系,以及解一元二次方程的方法,属于基础题.

练习册系列答案
相关题目
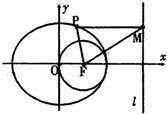 如图,F是椭圆的右焦点,以F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆的动点,P到两焦点距离之和等于4
如图,F是椭圆的右焦点,以F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆的动点,P到两焦点距离之和等于4