题目内容
设直线l的方程为(m2-2m-3)x+(2m2+m-1)y=2m-6,根据下列条件分别确定m的值.
(1)l在x轴上的截距是-3;
(2)l的斜率是-1.
(1)l在x轴上的截距是-3;
(2)l的斜率是-1.
分析:(1)由l在x轴上的截距是-3,可得
解出即可;
(2)由l的斜率是-1.可得
,解出即可.
|
(2)由l的斜率是-1.可得
|
解答:解:(1)由题意可得
由①可得m≠-1,m≠3.
由②得m=3或m=-
.
∴m=-
.
(2)由题意得
由③得:m≠-1,m≠
,
由④得:m=-1或m=-2.
∴m=-2.
|
由①可得m≠-1,m≠3.
由②得m=3或m=-
| 5 |
| 3 |
∴m=-
| 5 |
| 3 |
(2)由题意得
|
由③得:m≠-1,m≠
| 1 |
| 2 |
由④得:m=-1或m=-2.
∴m=-2.
点评:本题考查了斜率的计算公式、截距的意义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
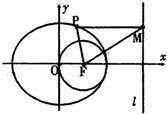 如图,F是椭圆的右焦点,以F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆的动点,P到两焦点距离之和等于4
如图,F是椭圆的右焦点,以F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆的动点,P到两焦点距离之和等于4