题目内容
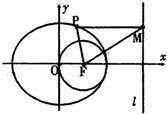 如图,F是椭圆的右焦点,以F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆的动点,P到两焦点距离之和等于4
如图,F是椭圆的右焦点,以F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆的动点,P到两焦点距离之和等于4(Ⅰ)求椭圆和圆的标准方程;
(Ⅱ)设直线l的方程为x=4,PM⊥l,垂足为M,是否存在点P,使得△FPM为等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.
分析:(Ⅰ)由已知可得2a=4,a=2c,由此能求出椭圆的标准方程和圆的标准方程.
(Ⅱ)设P(x,y),则由题设知
+
=1.由|PF|=
|PM|,|PF|≠|PM|,知若|PF|=|FM|,则|PF|+|FM|=|PM|这与三角形两边之和大于第三边矛盾,|PF|≠|PM|.若|PM|=|FM|,则(x-4)2=12-
x2,由此解得存在两点P(
,
),P(
,-
)使得△PFM为等腰三角形.
(Ⅱ)设P(x,y),则由题设知
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 4 |
| 7 |
| 3 |
| 7 |
| 15 |
| 4 |
| 7 |
| 3 |
| 7 |
| 15 |
解答:解:(Ⅰ)由已知可得2a=4,a=2c?a=2,c=1,b2=a2-c2=3
∴椭圆的标准方程为
+
=1,圆的标准方程为(x-1)2+y2=1
(Ⅱ)设P(x,y),则M(4,y),F(1,0)
∵P(x,y)在椭圆上∴
+
=1?y2=
x2.
|PF|2=(x-1)2+y2=(x-1)2+3-
x2=
(x-4)2
|PM|2=|x-4|2,9+y2=12-
x2
∴|PF|=
|PM|,|PF|≠|PM|
(1)若|PF|=|FM|则|PF|+|FM|=|PM|这与三角形两边之和大于第三边矛盾
∴|PF|≠|PM|
(2)若|PM|=|FM|,则(x-4)2=12-
x2,解得x=4或x=
∵|x|≤2∴x=
∴y=±
∴P(
,±
)
综上可得存在两点P(
,
),P(
,-
)使得△PFM为等腰三角形.
∴椭圆的标准方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)设P(x,y),则M(4,y),F(1,0)
∵P(x,y)在椭圆上∴
| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
| 4 |
|PF|2=(x-1)2+y2=(x-1)2+3-
| 3 |
| 4 |
| 1 |
| 4 |
|PM|2=|x-4|2,9+y2=12-
| 3 |
| 4 |
∴|PF|=
| 1 |
| 2 |
(1)若|PF|=|FM|则|PF|+|FM|=|PM|这与三角形两边之和大于第三边矛盾
∴|PF|≠|PM|
(2)若|PM|=|FM|,则(x-4)2=12-
| 3 |
| 4 |
| 4 |
| 7 |
∵|x|≤2∴x=
| 4 |
| 7 |
| 3 |
| 7 |
| 15 |
| 4 |
| 7 |
| 3 |
| 7 |
| 15 |
综上可得存在两点P(
| 4 |
| 7 |
| 3 |
| 7 |
| 15 |
| 4 |
| 7 |
| 3 |
| 7 |
| 15 |
点评:本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细求解.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目

