题目内容
(理)设整数m是从不等式x2-2x-8≤0的整数解的集合S中随机抽取的一个元素,记随机变量ξ=m2,则ξ的数学期望Eξ=(文)已知集合A={x|-1<x<5,x∈Z},集合B={x|
| x-1 | 4-x |
分析:(理)先解不等式x2-2x-8≤0的整数解的集合S,再由随机变量ξ=m2,求出分布列,用公式求出期望;
(文)求出集合B,进而利用交集的定义求出两个集合的交集,由古典概率模型公式求出概率.
(文)求出集合B,进而利用交集的定义求出两个集合的交集,由古典概率模型公式求出概率.
解答:解:(理)由x2-2x-8≤0得-2≤x≤4,符合条件的整数解的集合S={-2,-1,0,1,2,3,4}
∵ξ=m2,故变量可取的值分别为0,1,4,9,16,相应的概率分别为
,
,
,
,
∴ξ的数学期望Eξ=0×
+1×
+4×
+9×
+16×
=
=5
故答案为5
(文)由题意A={0,1,2,3,4},B={x|
>0,x∈Z}={2,3}
故A∩B={2,3}
∴在集合A中任取一个元素x,则事件“x∈A∩B”发生的概率是
故答案为:
.
∵ξ=m2,故变量可取的值分别为0,1,4,9,16,相应的概率分别为
| 1 |
| 7 |
| 2 |
| 7 |
| 2 |
| 7 |
| 1 |
| 7 |
| 1 |
| 7 |
∴ξ的数学期望Eξ=0×
| 1 |
| 7 |
| 2 |
| 7 |
| 2 |
| 7 |
| 1 |
| 7 |
| 1 |
| 7 |
| 35 |
| 7 |
故答案为5
(文)由题意A={0,1,2,3,4},B={x|
| x-1 |
| 4-x |
故A∩B={2,3}
∴在集合A中任取一个元素x,则事件“x∈A∩B”发生的概率是
| 2 |
| 5 |
故答案为:
| 2 |
| 5 |
点评:本题考查随机变量的期望与方差,解题的关键是理解所研究的事件类型确定求概率的方法,有公式求出概率.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
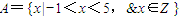 ,集合
,集合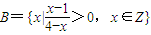 .在集合A中任取一个元素x,则事件“x∈A∩B”发生的概率是 .
.在集合A中任取一个元素x,则事件“x∈A∩B”发生的概率是 .