题目内容
(2011•黄冈模拟)若曲线f(x,y)=0(或y=f(x))在其上两个不同的点处的切线重合,则称这条切线为曲线f(x,y)=0(或y=f(x))的自公切线,则下列方程的曲线存在自公切线的有
①|x|+1=
②y2-x2 ③y=2sinx-3cosx ④y=xcosx.
③④
③④
(填上所有正确的序号)①|x|+1=
| 4-y2 |
分析:根据曲线存在自公切线的定义,分别画出①|x|+1=
②y2-x2=1③y=2sinx-3cosx ④y=xcosx.四个曲线的图形,观察图形得:③y=2sinx-3cosx ④y=xcosx.它们存在自公切线.
| 4-y2 |
解答: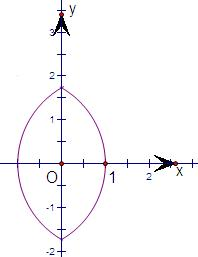 解:分别画出①|x|+1=
解:分别画出①|x|+1=
②y2-x2=1③y=2sinx-3cosx ④y=xcosx.四个曲线的图形,
观察图形得:③y=2sinx-3cosx ④y=xcosx.它们存在自公切线.
故答案为:③④.
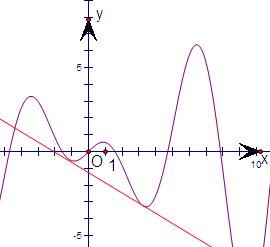
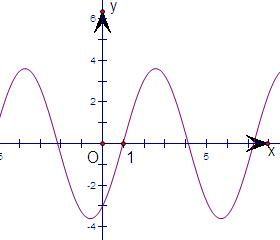
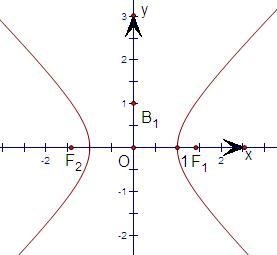
 解:分别画出①|x|+1=
解:分别画出①|x|+1=| 4-y2 |
观察图形得:③y=2sinx-3cosx ④y=xcosx.它们存在自公切线.
故答案为:③④.



点评:本小题主要考查曲线与方程、函数图象的应用等基础知识,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2011•黄冈模拟)已知:如图
(2011•黄冈模拟)已知:如图 (2011•黄冈模拟)分形几何学是美籍法国数学家伯努瓦••B•曼德尔布罗特(Benoit B.Mandelbrot) 在20世纪70年代创立的一门新学科,它的创立,为解决传统科学众多领域的难题提供了全新的思路.下图按照的分形
(2011•黄冈模拟)分形几何学是美籍法国数学家伯努瓦••B•曼德尔布罗特(Benoit B.Mandelbrot) 在20世纪70年代创立的一门新学科,它的创立,为解决传统科学众多领域的难题提供了全新的思路.下图按照的分形 规律生长成一个树形图,则第10行的空心圆点的个数是( )
规律生长成一个树形图,则第10行的空心圆点的个数是( )