题目内容
(本小题满分13分)已知集合A=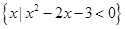 ,B=
,B=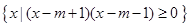 ,
,
(Ⅰ)当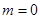 时,求
时,求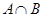 .
.
(Ⅱ)若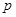 :
: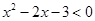 ,
,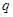 :
: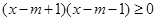 ,且
,且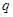 是
是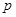 的必要不充分条件,求实数
的必要不充分条件,求实数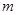 的取值范围。
的取值范围。
【答案】
(Ⅰ)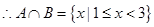 ;(Ⅱ)
;(Ⅱ)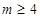 或
或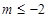
【解析】
试题分析:(1)当m=0时,求解集合B中一元二次不等式的解集,然后利用集合的交集运算得到结论。
(2)因为根据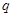 是
是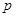 的必要不充分条件,则说明p,q命题表示的集合A,B之间有包含关系,且前者包含于后者。
的必要不充分条件,则说明p,q命题表示的集合A,B之间有包含关系,且前者包含于后者。
(Ⅰ):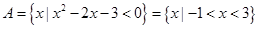 ,
,
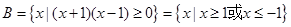
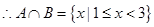
(Ⅱ) 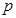 为:
为: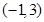
而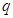 为:
为:
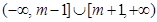 ,
,
又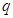 是
是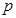 的必要不充分条件, 即
的必要不充分条件, 即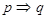
所以 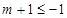 或
或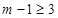
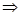
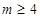 或
或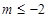
考点:本试题主要考查了一元二次不等式的解集和充分条件的判定的综合运用。
点评:解决该试题的关键是对于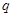 是
是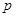 的必要不充分条件,那么对应到集合关系上,即为p时q的充分不必要,那么说明了p
的必要不充分条件,那么对应到集合关系上,即为p时q的充分不必要,那么说明了p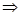 q
q

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目

 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和