题目内容
若a,b,m,n都为正实数,且m+n=1.
求证: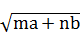 ≥m
≥m +n
+n .
.
见解析
解析证明:因为(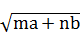 )2-(m
)2-(m +n
+n )2
)2
=ma+nb-m2a-n2b-2mn
=m(1-m)a+n(1-n)b-2mn
=mn( -
- )2≥0,
)2≥0,
又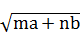 >0,m
>0,m +n
+n >0,
>0,
所以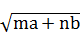 ≥m
≥m +n
+n .
.

练习册系列答案
相关题目
题目内容
若a,b,m,n都为正实数,且m+n=1.
求证: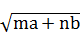 ≥m
≥m +n
+n .
.
见解析
解析证明:因为(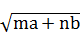 )2-(m
)2-(m +n
+n )2
)2
=ma+nb-m2a-n2b-2mn
=m(1-m)a+n(1-n)b-2mn
=mn( -
- )2≥0,
)2≥0,
又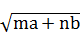 >0,m
>0,m +n
+n >0,
>0,
所以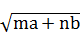 ≥m
≥m +n
+n .
.
