题目内容
已知f(x)在(-1,1)上有定义,f(| 1 |
| 2 |
| x+y |
| 1+xy |
(1)证明:f(x)在(-1,1)上为奇函数;?
(2)对数列x1=
| 1 |
| 2 |
| 2xn |
| 1+xn2 |
(3)求证
| 1 |
| f(x1) |
| 1 |
| f(x2) |
| 1 |
| f(xn) |
| 2n+5 |
| n+2 |
分析:(1)利用题中条件找出f(-x)=-f(x)即可
(2)找f(xn+1)与f(xn)的关系,得f(xn)的表达式
(3)利用等比数列的求和公式可得不等式的左边,再利用分离常数法把不等式的右边整理即可得结论
(2)找f(xn+1)与f(xn)的关系,得f(xn)的表达式
(3)利用等比数列的求和公式可得不等式的左边,再利用分离常数法把不等式的右边整理即可得结论
解答:(Ⅰ)证明:令x=y=0,∴2f(0)=f(0),∴f(0)=0
令y=-x,则f(x)+f(-x)=f(0)=0
∴f(x)+f(-x)=0∴f(-x)=-f(x)
∴f(x)为奇函数(4分)
(Ⅱ)解:f(x1)=f(
)=-1,f(xn+1)=f(
)=f(
)=f(xn)+f(xn)=2f(xn)
∴
=2即{f(xn)}是以-1为首项,2为公比的等比数列
∴f(xn)=-2n-1
(Ⅲ)解:
+
++
=(1+
+
++
)=-
=-(2-
)=-2+
>-2
而-
=-(2+
)=-2-
<-2
∴
+
++
>-
令y=-x,则f(x)+f(-x)=f(0)=0
∴f(x)+f(-x)=0∴f(-x)=-f(x)
∴f(x)为奇函数(4分)
(Ⅱ)解:f(x1)=f(
| 1 |
| 2 |
| 2xn |
| 1+xn2 |
| xn+xn |
| 1+xn•x n |
∴
| f(xn+1) |
| f(xn) |
∴f(xn)=-2n-1
(Ⅲ)解:
| 1 |
| f(x1) |
| 1 |
| f(x2) |
| 1 |
| f(xn) |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
1-
| ||
1-
|
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
而-
| 2n+5 |
| n+2 |
| 1 |
| n+2 |
| 1 |
| n+2 |
∴
| 1 |
| f(x1) |
| 1 |
| f(x2) |
| 1 |
| f(xn) |
| 2n+5 |
| n+2 |
点评:证明抽象函数的奇偶性,须利用函数奇偶性的定义,找准方向,巧妙赋值,合理,灵活变形,找出f(-x)与f(x)的关系.

练习册系列答案
相关题目
 ,且满足x,y∈(-1,1)有
,且满足x,y∈(-1,1)有 .对数列{xn}有
.对数列{xn}有
 <
< 成立?若存在,求出m的最小值.
成立?若存在,求出m的最小值.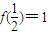 ,且满足x,y∈(-1,1)有
,且满足x,y∈(-1,1)有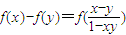 .对数列{xn}有
.对数列{xn}有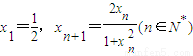
 <
<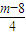 成立?若存在,求出m的最小值.
成立?若存在,求出m的最小值.