题目内容
已知f(x)在(-1,1)上有定义,f(| 1 |
| 2 |
| x-y |
| 1-xy |
| 1 |
| 2 |
| 2xn | ||
1+
|
(1)证明:f(x)在(-1,1)上为奇函数.
(2)求f(xn)的表达式.
(3)是否存在自然数m,使得对于任意n∈N*且
| 1 |
| f(x1) |
| 1 |
| f(x2) |
| 1 |
| f(xn) |
| m-8 |
| 4 |
分析:(1)先令x=y=0,解得f(0),再令x=0得f(0)-f(y)=f(-y)即f(y)+f(-y)=0由奇偶性定义判断.
(2)由x1=
,xn+1=
(n∈N*)易知0<xn<1,由主条件得f(xn)-f(-xn)=f(
)和f(x)在(-1,1)上为奇函数得f(xn+1)=2f(xn)再由f(x1)=1,得到f(xn)是以1为首项,2为公比的等比数列求解.
(3)由(2)将
+
++
<
成立转化为2-
<
恒成立,由2-
<2得
≥2求解.
(2)由x1=
| 1 |
| 2 |
| 2xn | ||
1+
|
| 2xn | ||
1+
|
(3)由(2)将
| 1 |
| f(x1) |
| 1 |
| f(x2) |
| 1 |
| f(xn) |
| m-8 |
| 4 |
| 1 |
| 2n-1 |
| m-8 |
| 4 |
| 1 |
| 2n-1 |
| m-8 |
| 4 |
解答:解:(1)当x=y=0时,f(0)=0,再令x=0得f(0)-f(y)=f(-y)即f(y)+f(-y)=0
∴f(x)在(-1,1)上为为奇函数.
(2)由x1=
,xn+1=
(n∈N*)易知:{xn}中0<xn<1,
∵f(xn)-f(-xn)=f(
)且f(x)在(-1,1)上为奇函数
∴f(xn+1)=2f(xn)由f(
)=1,x1=
∴f(x1)=1
∴f(xn)是以1为首项,2为公比的等比数列∴f(xn)=2n-1
(3)
+
++
=1+
+
++
=2-
假设存在m使得
+
++
<
成立,即2-
<
恒成立,
∵2-
<2,
∴
≥2,
∴m≥16,
∴存在自然数m≥16,
使得
+
++
<
成立,此时最小的自然数m=16.
∴f(x)在(-1,1)上为为奇函数.
(2)由x1=
| 1 |
| 2 |
| 2xn | ||
1+
|
∵f(xn)-f(-xn)=f(
| 2xn | ||
1+
|
∴f(xn+1)=2f(xn)由f(
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x1)=1
∴f(xn)是以1为首项,2为公比的等比数列∴f(xn)=2n-1
(3)
| 1 |
| f(x1) |
| 1 |
| f(x2) |
| 1 |
| f(xn) |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
假设存在m使得
| 1 |
| f(x1) |
| 1 |
| f(x2) |
| 1 |
| f(xn) |
| m-8 |
| 4 |
| 1 |
| 2n-1 |
| m-8 |
| 4 |
∵2-
| 1 |
| 2n-1 |
∴
| m-8 |
| 4 |
∴m≥16,
∴存在自然数m≥16,
使得
| 1 |
| f(x1) |
| 1 |
| f(x2) |
| 1 |
| f(xn) |
| m-8 |
| 4 |
点评:本题主要考查抽象抽象函数判断奇偶性及求解析式,进而转化为数列模型研究等比数列求和解决恒成立问题.

练习册系列答案
相关题目
 ,且满足x,y∈(-1,1)有
,且满足x,y∈(-1,1)有 .对数列{xn}有
.对数列{xn}有
 <
< 成立?若存在,求出m的最小值.
成立?若存在,求出m的最小值.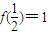 ,且满足x,y∈(-1,1)有
,且满足x,y∈(-1,1)有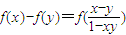 .对数列{xn}有
.对数列{xn}有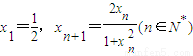
 <
<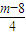 成立?若存在,求出m的最小值.
成立?若存在,求出m的最小值.