题目内容
已知f（x）在（-1，1）上有定义，f(
)=-1且满足x，y∈（-1，1）时，有f(x)+f(y)=f(
)
（1）证明：f（x）在（-1，1）上为奇函数．
（2）数列{an}满足a1=
，an+1=
，xn=f（an），求{xn}的通项公式．
（3）求证：1+f(
)+f(
)+…+f(
)=-f(
)．
| 1 |
| 2 |
| x+y |
| 1+xy |
（1）证明：f（x）在（-1，1）上为奇函数．
（2）数列{an}满足a1=
| 1 |
| 2 |
| 2an |
| 1+an2 |
（3）求证：1+f(
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| n2+3n+1 |
| 1 |
| n+2 |
分析：利用赋值法，先令y=0可求f（0）=0，再令y=-x即可证明f（-x）=-f（x），即可
（2）由xn=f(an)=f(
)=f（an-1）+f（an-1）=2f（an-1）=2xn-1，可得{xn}为等比数列，根据等比数列的通项公式可求
（3）由
=
=
及f（x+y）=f（
）可得f(
)=f(
)+f(-
)=f(
)-f(
)，利用叠加可求
（2）由xn=f(an)=f(
| 2an-1 |
| 1+an-12 |
（3）由
| 1 |
| n2+3n+1 |
| (n+2)-(n+1) |
| (n+2)(n+1)-1 |
| ||||
1+
|
| x+y |
| 1+xy |
| 1 |
| n2+3n+1 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
解答：（1）证明：令y=0得：f（x）+f（0）=f（x）所以f（0）=0
令y=-x得：f（x）+f（-x）=f（0）=0所以f（-x）=-f（x）
又f（x）的定义域为（-1，1）
所以f（x）在（-1，1）上为奇函数
（2）解：∵xn=f(an)=f(
)=f（an-1）+f（an-1）=2f（an-1）=2xn-1
x1=f(a1)=f(
)=-1
所以{xn}为以2为公比-1为首项的等比数列． 故xn=-2n-1
（3）证明：∵
=
=
所以：f(
)=f(
)+f(-
)=f(
)-f(
)
所以 f(
)=f(
)-f(
)
f(
)=f(
)-f(
)
…
f(
)=f(
)-f(
)
以上等式相加得：1+f(
)+f(
)+…f(
)=1+f(
)-f(
)=-f(
)
令y=-x得：f（x）+f（-x）=f（0）=0所以f（-x）=-f（x）
又f（x）的定义域为（-1，1）
所以f（x）在（-1，1）上为奇函数
（2）解：∵xn=f(an)=f(
| 2an-1 |
| 1+an-12 |
x1=f(a1)=f(
| 1 |
| 2 |
所以{xn}为以2为公比-1为首项的等比数列． 故xn=-2n-1
（3）证明：∵
| 1 |
| n2+3n+1 |
| (n+2)-(n+1) |
| (n+2)(n+1)-1 |
| ||||
1+
|
所以：f(
| 1 |
| n2+3n+1 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
所以 f(
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
f(
| 1 |
| 11 |
| 1 |
| 3 |
| 1 |
| 4 |
…
f(
| 1 |
| n2+3n+1 |
| 1 |
| n+1 |
| 1 |
| n+2 |
以上等式相加得：1+f(
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| n2+3n+1 |
| 1 |
| 2 |
| 1 |
| n+2 |
| 1 |
| n+2 |
点评：本题主要考查了利用赋值法证明抽象函数的奇偶性，及等比数列的证明，通项公式的求解，叠加求解数列的和，本题是函数与数列知识的综合应用，具有一定的综合性．
练习册系列答案
阅读快车系列答案
相关题目
，且满足x，y∈（-1，1）有
．对数列{xn}有
＜
成立？若存在，求出m的最小值．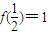
，且满足x，y∈（-1，1）有
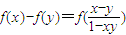．对数列{xn}有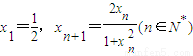
＜
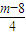成立？若存在，求出m的最小值．