题目内容
已知
是定义在
上的奇函数，当
时，
，则在上
的表达式为
A． | B． | C． | D． |
B
解析试题分析：因为设x＜0，则-x＞0，由f（x）为奇函数知f（x）=-f（-x）=-[（-x）2-2（-x）]=-x2-2x，
所以可知函数
即f（x）=x（|x|-2），选B.
考点：本试题主要考查了函数的奇偶性的运用，求解对称区间的函数的解析式。
点评：解决该试题的关键是理解当x<0时，那么将-x>0，满足 已知条件，得到函数f(-x)的解析式，进而结合奇函数的定义得到f(x).
练习册系列答案
怎样学好牛津英语系列答案
相关题目
的图象为
的部分图象大致是图中的 （ ）
将函数
在
上的所有极值点按从小到大排成一列
，给出以下不等式： ①
； ②
；③
；④
；其中，正确的判断是（ ）
| A．①③ | B．①④ | C．②③ | D．②④ |
直角梯形ABCD如图（1），动点P从B点出发，由B→C→D→A沿边运动，设点P运动的距离为x，ΔABP面积为f(x).若函数y= f(x)的图象如图（2），则ΔABC的面积为 （ ）
| A．10 | B．16 | C．18 | D．32 |
的一个正数零点附近的函数值用二分法逐次计算，参考数据如下表：
的一个近似根（精确度为0.05）为（ ）函数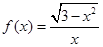
的图象关于（ ）对称
| A．原点 | B．x轴 | C．y轴 | D．直线 |
与指数函数
的图象只可能是（ ）
函数
的零点所在的区间是 （ ）
A． | B． | C． | D． |