题目内容
14.在平面直角坐标系xOy中,若动点P(a,b)到直线l1:y=x,l2:y=-x+1的距离分别为d1,d2,且满足d1+2d2=2√2√2,则a2+b2的最大值为172172.分析 利用点到直线的距离公式可得:|a-b|+2|a+b-1|=4.通过分类讨论可知:点(a,b)是如图所示的四边形的4条边.即可得到√a2+b2√a2+b2最大值.
解答 解:∵动点P(a,b)到两直线l1:y=x和l2:y=-x+的距离为d1,d2,且满足d1+2d2=2√2√2,
∴|a−b|√2|a−b|√2+2×|a+b−1|√2|a+b−1|√2=2√2√2,
化为|a-b|+2|a+b-1|=4.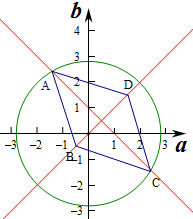
分为以下4种情况:
①{a−b≥0a+b−1≥03a+b−6=0⎧⎪⎨⎪⎩a−b≥0a+b−1≥03a+b−6=0
②{a−b≥0a+b−1<0a+3b+2=0,
③{a−b<0a+b−1≥0a+3b−6=0,
④{a−b<0a+b−1<03a+b+2=0.
可知点(a,b)是如图所示的四边形的4条边.
可知:当取点A或C时,√a2+b2取得最大值,
由{3a+b−6=0a+b−1=0得{a=52b=−32,
即C(52,-32),
此时a2+b2=(52)2+(-32)2=254+94=344=172.
故答案为:172
点评 本题考查了点到直线的距离公式、含绝对值的等式、分类讨论等基础知识与基本技能方法,难度较大.

练习册系列答案
相关题目
2.椭圆x216+y29=1的焦点的坐标为( )
| A. | (0,5)和(0,-5) | B. | (√7,0)和(-√7,0) | C. | (0,√7) | D. | (5,0)和(-5,0) |
6.已知a>b>0,那么下列不等式成立的是( )
| A. | -a>-b | B. | a+c<b+c | C. | a2>b2 | D. | 1a>1b |
3.下列4个不等式:
(1)∫10√xdx<∫10\root{3}{x}dx;
(2)∫π40sinxdx<∫π40cosxdx;
(3)∫10e-xdx<∫10e−x2dx;
(4)∫20sinxdx<∫20xdx.
能够成立的个数是( )
(1)∫10√xdx<∫10\root{3}{x}dx;
(2)∫π40sinxdx<∫π40cosxdx;
(3)∫10e-xdx<∫10e−x2dx;
(4)∫20sinxdx<∫20xdx.
能够成立的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4. 如图,在四边形ABCD中,AB=CD=1,BC=√3,且∠B=90°,∠BCD=120°,记向量→AB=→a,→AC=→b,则→AD=( )
如图,在四边形ABCD中,AB=CD=1,BC=√3,且∠B=90°,∠BCD=120°,记向量→AB=→a,→AC=→b,则→AD=( )
 如图,在四边形ABCD中,AB=CD=1,BC=√3,且∠B=90°,∠BCD=120°,记向量→AB=→a,→AC=→b,则→AD=( )
如图,在四边形ABCD中,AB=CD=1,BC=√3,且∠B=90°,∠BCD=120°,记向量→AB=→a,→AC=→b,则→AD=( )| A. | 2√33→a-(1+√36)→b | B. | -2√33→a+(1+√36)→b | C. | -2√33→a+(1-√36)→b | D. | 2√33→a+(1+√36)→b |