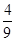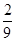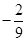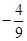题目内容
(本小题共9分)
已知函数f(x)=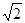 sin(2x+
sin(2x+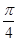 ),x∈R.
),x∈R.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x)在区间[-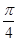 ,
,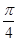 ]上的最大值和最小值。
]上的最大值和最小值。
已知函数f(x)=
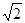 sin(2x+
sin(2x+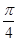 ),x∈R.
),x∈R.(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x)在区间[-
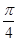 ,
,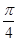 ]上的最大值和最小值。
]上的最大值和最小值。(1)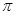 (2)最大值为
(2)最大值为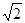 ,最小值为-1
,最小值为-1
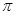 (2)最大值为
(2)最大值为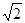 ,最小值为-1
,最小值为-1试题分析:解:(Ⅰ)f(x)的最小正周期T=
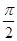 =
=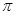 3分
3分(Ⅱ)因为f(x)在区间[-
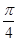 ,
,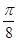 ]上是增函数,在区间[
]上是增函数,在区间[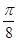 ,
,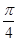 ]上是减函数,又f(-
]上是减函数,又f(-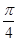 )=-1,f(
)=-1,f(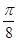 )=
)=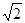 ,f(
,f(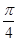 )=1,故函数f(x)在区间[-
)=1,故函数f(x)在区间[-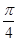 ,
,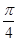 ]上的最大值为
]上的最大值为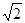 ,最小值为-1。 9分
,最小值为-1。 9分点评:解决的关键是能根据解析式结合周期公式得到周期,同时能根据定义域求解函数的值域,属于基础题。

练习册系列答案
相关题目
 的部分图象如图所示,则
的部分图象如图所示,则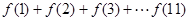 的值等于 ( )
的值等于 ( )

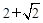
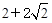
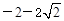
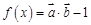 ,其中向量
,其中向量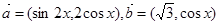 , (
, (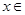 R).
R).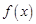 的最小正周期和最小值;
的最小正周期和最小值;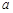 、
、 、
、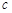 ,若
,若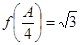 ,a=2
,a=2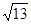 ,
,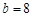 ,求边长
,求边长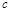 的值.
的值.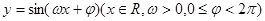 的部分图象如图,则
的部分图象如图,则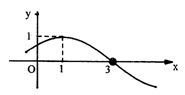
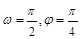
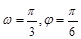
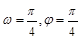
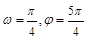
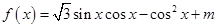
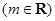 的图象过点
的图象过点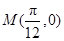 .
. 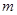 的值;
的值;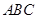 中,角
中,角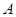 ,
,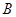 ,
,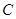 的对边分别是
的对边分别是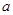 ,
,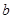 ,
,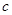 .若
.若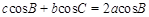 ,求
,求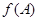 的取值范围.
的取值范围. ,则tan2α等于( )
,则tan2α等于( )



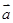 =(
=(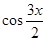 ,
,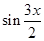 ),
),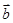 =(
=(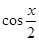 ,-
,-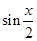 ),且
),且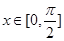 .
. ,且
,且 ,则
,则 的值为 ;
的值为 ;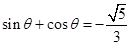 ,则
,则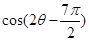 的值为( )
的值为( )