题目内容
(本小题满分12分)
已知向量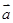 =(
=(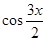 ,
,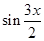 ),
),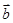 =(
=(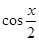 ,-
,-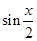 ),且
),且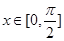 .
.
(Ⅰ)用cosx表示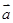 ·
·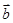 及|
及|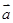 +
+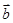 |;
|;
(Ⅱ)求函数f(x)=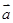 ·
·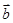 +2|
+2|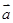 +
+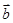 |的最小值.
|的最小值.
已知向量
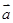 =(
=(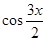 ,
,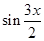 ),
),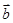 =(
=(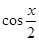 ,-
,-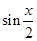 ),且
),且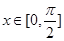 .
.(Ⅰ)用cosx表示
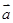 ·
·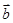 及|
及|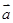 +
+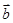 |;
|;(Ⅱ)求函数f(x)=
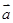 ·
·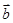 +2|
+2|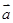 +
+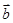 |的最小值.
|的最小值.(Ⅰ)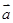 ·
·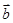 =2cos2x-1,|
=2cos2x-1,|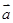 +
+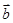 |=2
|=2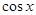 .
.
(Ⅱ)当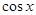 =0时,f(x)取得最小值-1.
=0时,f(x)取得最小值-1.
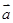 ·
·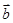 =2cos2x-1,|
=2cos2x-1,|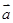 +
+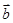 |=2
|=2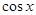 .
.(Ⅱ)当
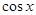 =0时,f(x)取得最小值-1.
=0时,f(x)取得最小值-1.试题分析:(Ⅰ)
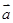 ·
·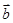 =
=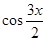
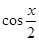 -
-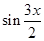
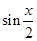 =
=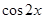 =2cos2x-1,
=2cos2x-1, |
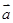 +
+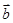 |=
|=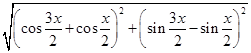 =
=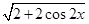 =2|
=2|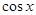 |,
|,∵
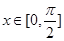 ,∴
,∴ 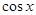 ≥0,∴ |
≥0,∴ |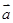 +
+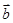 |=2
|=2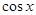 .
.(Ⅱ)f(x)=
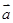 ·
·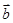 +2|
+2|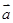 +
+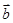 |=2cos2x-1+4
|=2cos2x-1+4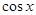 =2(
=2(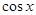 +1)2-3,
+1)2-3, ∵
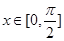 ,∴ 0≤
,∴ 0≤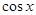 ≤1, ∴ 当
≤1, ∴ 当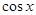 =0时,f(x)取得最小值-1.
=0时,f(x)取得最小值-1.点评:以向量为背景考查三角函数的化简及性质是近两年考试的热点,既考查了向量的坐标运算,又考查了三角函数的性质及最值。

练习册系列答案
相关题目
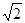 sin(2x+
sin(2x+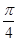 ),x∈R.
),x∈R.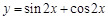 的图像向左平移
的图像向左平移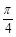 个单位长度,所得图像的解析式是
个单位长度,所得图像的解析式是



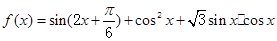 .
.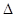 ABC的三个内角,若cosB=
ABC的三个内角,若cosB=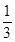 ,
,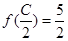 ,求sinA.
,求sinA.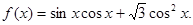
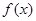 的最小正周期;
的最小正周期;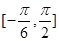 上的最大值和最小值.
上的最大值和最小值.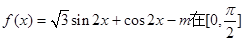 上有两个零点,则m的取值范围是
上有两个零点,则m的取值范围是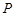 从
从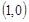 出发,沿单位圆逆时针方向运动
出发,沿单位圆逆时针方向运动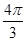 弧长到达
弧长到达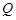 点,则
点,则



 的值为 .
的值为 .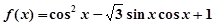 .
.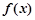 的单调递增区间;
的单调递增区间;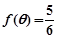 ,
,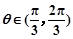 ,求
,求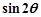 的值.
的值.