题目内容
已知三棱锥P-ABC的三个侧面与底面全等,且AB=AC=
,BC=2.则二面角P-BC-A的大小为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:要求二面角P-BC-A的大小,我们关键是要找出二面角P-BC-A的大小的平面角,将空间问题转化为平面问题,然后再分析二面角P-BC-A的大小的平面角所在的三角形的其它边与角的关系,解三角形进行求解.
解答:解:如图所示,由三棱锥的三个侧面与底面全等,
且AB=AC=
,
得PB=PC=
,PA=BC=2,
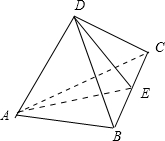
取BC的中点E,连接AE,PE,
则∠AEP即为所求二面角的平面角.
且AE=EP=
,
∵AP2=AE2+PE2,
∴∠AEP=
,
故选C.
且AB=AC=
| 3 |
得PB=PC=
| 3 |
取BC的中点E,连接AE,PE,
则∠AEP即为所求二面角的平面角.
且AE=EP=
| 2 |
∵AP2=AE2+PE2,
∴∠AEP=
| π |
| 2 |
故选C.

点评:求二面角的大小,一般先作出二面角的平面角.此题是利用二面角的平面角的定义作出∠AEP为二面角P-BC-A的平面角,通过解∠AEP所在的三角形求得∠AEP.其解题过程为:作∠AEP→证∠AEP是二面角的平面角→计算∠AEP,简记为“作、证、算”.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知三棱锥P-ABC中,PC⊥底面ABC,AB=BC,D、F分别为AC、PC的中点,DE⊥AP于E.
已知三棱锥P-ABC中,PC⊥底面ABC,AB=BC,D、F分别为AC、PC的中点,DE⊥AP于E. 如图,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB的中点,且△PDB是正三角形,PA⊥PC.
如图,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB的中点,且△PDB是正三角形,PA⊥PC. (2009•河西区二模)如图,已知三棱锥P-ABC中,PA⊥面ABC,其中正视图为Rt△PAC,AC=2
(2009•河西区二模)如图,已知三棱锥P-ABC中,PA⊥面ABC,其中正视图为Rt△PAC,AC=2 (2009•黄浦区二模)已知三棱锥P-ABC的棱长都是2,点D是棱AP上不同于P的点.
(2009•黄浦区二模)已知三棱锥P-ABC的棱长都是2,点D是棱AP上不同于P的点.