题目内容
 (2009•黄浦区二模)已知三棱锥P-ABC的棱长都是2,点D是棱AP上不同于P的点.
(2009•黄浦区二模)已知三棱锥P-ABC的棱长都是2,点D是棱AP上不同于P的点.(1)试用反证法证明直线BD与直线CP是异面直线.
(2)求三棱锥P-ABC的体积VP-ABC.
分析:(1)假设BD与CP不是异面直线,即BD与CP都在平面α上,从而可得出点A、B、C、P都在平面α上,这与P-ABC是三棱锥矛盾,故假设不成立,得证;
(2)求三棱锥P-ABC的体积VP-ABC.选△ABC为底,故关键是求出底面上的高,为此利用底面三角形是正三角形,可求.
(2)求三棱锥P-ABC的体积VP-ABC.选△ABC为底,故关键是求出底面上的高,为此利用底面三角形是正三角形,可求.
解答: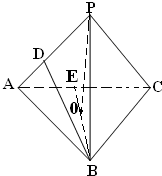 解:(1)证明:(反证法)假设BD与CP不是异面直线.(2分)
解:(1)证明:(反证法)假设BD与CP不是异面直线.(2分)
设BD与CP都在平面α上.∵P∈α,D∈α,∴PD?α.又A∈PD,∴A∈α.
∴点A、B、C、P都在平面α上,这与P、A、B、C不共面(P-ABC是三棱锥)矛盾,于是,假设不成立.(5分)
所以直线BD与CP是异面直线.(6分)
(2)设锥顶点P在底面的射影为O.∵P-ABC的棱长都是2,∴△ABC是正三角形.
∴AO=BO=CO(=
),
即O为底面三角形的中心,因此P-ABC为正三棱锥.连接BO并延长交AC于E,则BE⊥AC.
∵AB=BC=AC=PB=2,∴BE=ABsin60°=
. (8分)
∴BO=
,进一步可得PO=
=
=
. (10分)
∴VP-ABC=
S△ABC•PO
=
•
•
•2•2•sin60°
=
. (12分)
 解:(1)证明:(反证法)假设BD与CP不是异面直线.(2分)
解:(1)证明:(反证法)假设BD与CP不是异面直线.(2分)设BD与CP都在平面α上.∵P∈α,D∈α,∴PD?α.又A∈PD,∴A∈α.
∴点A、B、C、P都在平面α上,这与P、A、B、C不共面(P-ABC是三棱锥)矛盾,于是,假设不成立.(5分)
所以直线BD与CP是异面直线.(6分)
(2)设锥顶点P在底面的射影为O.∵P-ABC的棱长都是2,∴△ABC是正三角形.
∴AO=BO=CO(=
| PA2-PO2 |
即O为底面三角形的中心,因此P-ABC为正三棱锥.连接BO并延长交AC于E,则BE⊥AC.
∵AB=BC=AC=PB=2,∴BE=ABsin60°=
| 3 |
∴BO=
2
| ||
| 3 |
| PB2-BO2 |
4-
|
2
| ||
| 3 |
∴VP-ABC=
| 1 |
| 3 |
=
| 1 |
| 3 |
2
| ||
| 3 |
| 1 |
| 2 |
=
2
| ||
| 3 |
点评:本题的考点是反证法,主要考查反证法证明异面直线问题,关键是利用反证法的步骤,恰当反设,通过推理论证引出矛盾,考查三棱锥体积的计算,关键是选好底面,求出高.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目