题目内容
设f(x),g(x)分别是定义在R上的奇函数和偶函数.当x<0时,f'(x)g(x)+f(x)g'(x)>0,且g(-3)=0,则不等式
>0的解集是( )
| f(x) |
| g(x) |
分析:令F(x)=f(x)•g(x),则F′(x)>0,
解答:解:设F(x)=f (x)g(x),
当x<0时,?∵F′(x)=f′(x)g(x)+f (x)g′(x)>0,
∴F(x)在(-∞,0)上为增函数;
∵F(-x)=f (-x)g (-x)=-f (x)•g (x)=-F(x),?
∴F(x)为R上的奇函数,故F(x)在R上亦为增函数.?
∵g(-3)=0,必有F(-3)=F(3)=0.?
构造如图的F(x)=f (x)g(x)的图象,
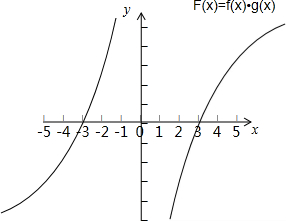
可知F(x)>0的解集为(-3,0)∪(3,+∞).
∵
>0?
>0?F(x)>0,
∴
>0的解集就是F(x)>0的解集(-3,0)∪(3,+∞).
故选A.
当x<0时,?∵F′(x)=f′(x)g(x)+f (x)g′(x)>0,
∴F(x)在(-∞,0)上为增函数;
∵F(-x)=f (-x)g (-x)=-f (x)•g (x)=-F(x),?
∴F(x)为R上的奇函数,故F(x)在R上亦为增函数.?
∵g(-3)=0,必有F(-3)=F(3)=0.?
构造如图的F(x)=f (x)g(x)的图象,
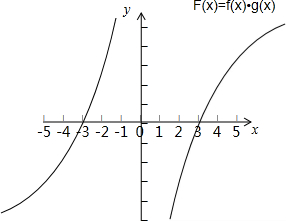
可知F(x)>0的解集为(-3,0)∪(3,+∞).
∵
| f(x) |
| g(x) |
| f(x)•g(x) |
| g2(x) |
∴
| f(x) |
| g(x) |
故选A.
点评:本题考查利用导数研究函数的单调性,考查构造函数思想与数形结合思想及等价转化思想的综合运用,考查推理分析与作图运算的能力,属于中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目