题目内容
设f（x），g（x）是实数集R上的奇函数，{x|f（x）＞0}={x|4＜x＜10}，{x|g（x）＞0}={x|2＜x＜5}，则集合{x|f（x）g（x）＞0}=
（4，5）∪（-5，-4）
（4，5）∪（-5，-4）
．分析：先根据f（x），g（x）都是R上的奇函数可确定它们的图象关于原点对称，画出示意图，进而可得到f（x），g（x）在什么范围内异号，结合函数图象可确定不等式f（x）•g（x）＞0的解集可求得答案．
解答：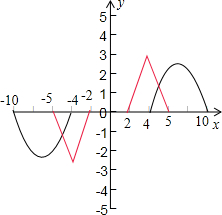
解：因f（x），g（x）都是R上的奇函数，它们的图象关于原点对称，画出示意图如图，
不等式f（x）•g（x）＞0表示f（x）与g（x）的符号相同，
观察图形，得出不等式f（x）•g（x）＞0的解集为：-5＜x＜-4或4＜x＜5．
故答案为（4，5）∪（-5，-4）．
解：因f（x），g（x）都是R上的奇函数，它们的图象关于原点对称，画出示意图如图，不等式f（x）•g（x）＞0表示f（x）与g（x）的符号相同，
观察图形，得出不等式f（x）•g（x）＞0的解集为：-5＜x＜-4或4＜x＜5．
故答案为（4，5）∪（-5，-4）．
点评：本题考查了交、并、补集的混合运算、函数的奇偶性的应用，不等式的解法等，利用数形结合的思想进行解题．属于中档题．
练习册系列答案
金钥匙试卷系列答案
相关题目