题目内容
10.给定区域D:$\left\{\begin{array}{l}{2x-y+k≥0}\\{x+y≥0}\\{x≤2}\end{array}\right.$,(k为非负实数),若对于区域D内的任意一个点M(x,y),恒有2x-5y+10k+15>0成立;且在区域D内存在点N(x0,y0),满足-7x0+2y0-5k2+2>0,则实数k的取值范围是( )| A. | [0,1) | B. | ($\frac{1}{5}$,1) | C. | [0,$\frac{1}{5}$) | D. | ($\frac{1}{5}$,+∞) |
分析 对于区域D内的任意一个点M(x,y),恒有2x-5y+10k+15>0成立可化为(2x-5y)min>-10k-15;在区域D内存在点N(x0,y0),满足-7x0+2y0-5k2+2>0可化为(-7x0+2y0)max>5k2-2;故由题意作出区域D,从而由线性规划化为最优解,从而求最值即可.
解答 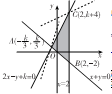 解:由题意作出区域D如图,且A(-$\frac{k}{3}$,$\frac{k}{3}$),B(2,-2),C(2,k+4),
解:由题意作出区域D如图,且A(-$\frac{k}{3}$,$\frac{k}{3}$),B(2,-2),C(2,k+4),
设z1=2x-5y,则y=$\frac{2}{5}$x-$\frac{1}{5}$z1,
当直线y=$\frac{2}{5}$x-$\frac{1}{5}$z1过点C(2,k+4)时,其在y轴上的截距-$\frac{1}{5}$z1最大,即z1最小为-5k-16,
由2x-5y+10k+15>0恒成立知,-5k-16>-10k-15,即k>$\frac{1}{5}$;
设z2=-7x+2y,则y=$\frac{7}{2}$x+$\frac{{z}_{2}}{2}$,
当直线y=$\frac{7}{2}$x+$\frac{{z}_{2}}{2}$过点A(-$\frac{k}{3}$,$\frac{k}{3}$)时,其在y轴上的截距$\frac{{z}_{2}}{2}$最大,即z2最大,此时z2=3k;
故存在点N(x0,y0),满足-7x0+2y0-5k2+2>0可化为3k-5k2+2>0,
故-$\frac{2}{5}$<k<1,
综上所述,$\frac{1}{5}$<k<1;
故选B.
点评 本题考查了简单线性规划,作图要细致认真,同时考查了恒成立问题及存在性问题,属于难题.

练习册系列答案
相关题目
5. 如图所示,已知直线l:y=kx-1(k>0)与抛物线C:x2=4y交与M,N两点,F为抛物线C的焦点,若|MF|=2|NF|,则实数k的值为( )
如图所示,已知直线l:y=kx-1(k>0)与抛物线C:x2=4y交与M,N两点,F为抛物线C的焦点,若|MF|=2|NF|,则实数k的值为( )
 如图所示,已知直线l:y=kx-1(k>0)与抛物线C:x2=4y交与M,N两点,F为抛物线C的焦点,若|MF|=2|NF|,则实数k的值为( )
如图所示,已知直线l:y=kx-1(k>0)与抛物线C:x2=4y交与M,N两点,F为抛物线C的焦点,若|MF|=2|NF|,则实数k的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{3\sqrt{2}}{4}$ |
15.在复平面内,复数z与$\frac{5}{i-2}$的对应点关于虚轴对称,则z=( )
| A. | 2+i | B. | 2-i | C. | -2+i | D. | -2-i |
2.已知函数 f(x)=$\frac{a}{x}+xlnx,g(x)={x^3}-{x^2}$-5,若对任意的 ${x_1},{x_2}∈[{\frac{1}{2},2}]$,都有f(x1)-g(x2)≥2成立,则a的取值范围是( )
| A. | (0,+∞) | B. | [1,+∞) | C. | (-∞,0) | D. | (-∞,-1] |