题目内容
10. 如图所示,已知棱锥V-ABC的底面积是64cm2,平行于底面的截面面积是4cm2,棱锥顶点V在截面和底面上的射影分别是O1,O,过O1O的三等分点作平行于底面的截面,求各截面的面积.
如图所示,已知棱锥V-ABC的底面积是64cm2,平行于底面的截面面积是4cm2,棱锥顶点V在截面和底面上的射影分别是O1,O,过O1O的三等分点作平行于底面的截面,求各截面的面积.
分析 利用面积的比s相似比的平方,求出VO1与VO的关系,然后求出VO2,VO3与VO的关系,推出截面面积即可.
解答 解:棱锥V-ABC的底面积是64cm2,平行于底面的截面面积是4cm2,棱锥顶点V在截面和底面上的射影分别是O1,O,S底=64,可得$\frac{4}{64}={(\frac{{VO}_{1}}{VO})}^{2}$,可得:$\frac{{VO}_{1}}{VO}=\frac{1}{4}$,过O1O的三等分点作平行于底面的截面,
可得VO2=$\frac{1}{2}VO$,过O2的截面面积为S2,则$\frac{{S}_{2}}{{S}_{底}}=\frac{1}{4}$,S2=16.
VO3=$\frac{3}{4}VO$,过O3的截面面积为S3,则$\frac{{S}_{3}}{{S}_{底}}=\frac{9}{16}$,S3=36.
所求截面面积分别为:16cm2,36cm2.
点评 本题考查棱锥的结构特征,几何体的面积与截面面积的求法,相似比与面积的比的关系是解题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
15.若正方体的体对角线长为4,则正方体的表面积为( )
| A. | $\frac{16}{3}$ | B. | 32 | C. | $\frac{64\sqrt{3}}{9}$ | D. | $\frac{128\sqrt{3}}{3}$ |
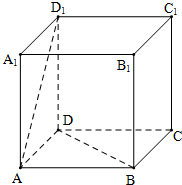 如图,正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是线段AD1和BD上的点,且D1P:PA=DQ:QB=5:12.
如图,正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是线段AD1和BD上的点,且D1P:PA=DQ:QB=5:12.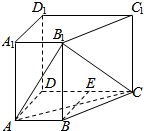 如图,在四棱锥ABCD-A1B1C1D中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0),现将与四棱锥ABCD-A1B1C1D形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱锥形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新的四棱柱中,记其中最小的表面积为f(k),写出f(k)的表达式.
如图,在四棱锥ABCD-A1B1C1D中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0),现将与四棱锥ABCD-A1B1C1D形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱锥形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新的四棱柱中,记其中最小的表面积为f(k),写出f(k)的表达式.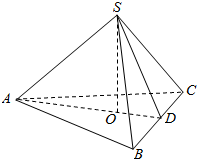
 如图,斜四边形ABCD-A1B1C1D1的底面是边长为8cm的正方形,侧棱AA1成为12cm,且上底面的顶点A1与下底面各点间的距离相等,则四棱柱的侧面积是$32\sqrt{15}$.
如图,斜四边形ABCD-A1B1C1D1的底面是边长为8cm的正方形,侧棱AA1成为12cm,且上底面的顶点A1与下底面各点间的距离相等,则四棱柱的侧面积是$32\sqrt{15}$.