题目内容
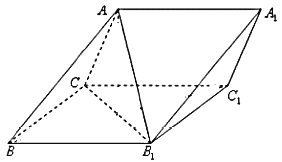
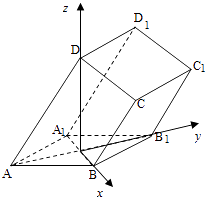
【题目】如图所示，在四棱柱ABCD﹣A1B1C1D1中，底面ABCD是梯形，AD∥BC，侧面ABB1A1为菱形，∠DAB=∠DAA1 ． 
（1）求证：A1B⊥AD；
（2）若AD=AB=2BC，∠A1AB=60°，点D在平面ABB1A1上的射影恰为线段A1B的中点，求平面DCC1D1与平面ABB1A1所成锐二面角的余弦值．
【答案】
（1）证明：通过条件可知 
= 
、∠DAB=∠DAA1，利用 
=即得A1B⊥AD；
（2）解：设线段A1B的中点为O，连接DO、AB1，
由题意知DO⊥平面ABB1A1．
因为侧面ABB1A1为菱形，所以AB1⊥A1B，
故可分别以射线OB、射线OB1、射线OD为x轴、y轴、z轴
的正方向建立空间直角坐标系O﹣xyz，如图所示．
设AD=AB=2BC=2a，由∠A1AB=60°可知|0B|=a， 
，
所以 
=a，从而A（0， 
a，0），B（a，0，0），
B1（0， 
a，0），D（0，0，a），所以 
= 
=（﹣a， a，0）．
由 
可得C（a， 
a， 
a），所以 
=（a， a，﹣ a），
设平面DCC1D1的一个法向量为 
=（x0，y0，z0），
由 = =0，得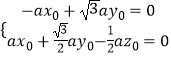 
，
取y0=1，则x0= ，z0=3 ，所以 =（ ，1，3 ）．
又平面ABB1A1的法向量为 
=D（0，0，a），
所以 
= 
= 
= 
，
故平面DCC1D1与平面ABB1A1所成锐二面角的余弦值为 ．
【解析】（1）通过已知条件易得 = 、∠DAB=∠DAA1 ， 利用 =0即得A1B⊥AD；（2）通过建立空间直角坐标系O﹣xyz，平面DCC1D1与平面ABB1A1所成锐二面角的余弦值即为平面ABB1A1的法向量与平面DCC1D1的一个法向量的夹角的余弦值，计算即可．
【考点精析】解答此题的关键在于理解直线与平面垂直的性质的相关知识，掌握垂直于同一个平面的两条直线平行．
