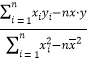题目内容
【题目】△ABC的内角A，B，C的对边分别为a，b，c，已知2cosC（acosB+bcosA）=c．
（1）求C；
（2）若 
的面积为 
，求△ABC的周长．
【答案】
（1）
解：（Ⅰ）已知等式利用正弦定理化简得：2cosC（sinAcosB+sinBcosA）=sinC，
整理得：2cosCsin（A+B）=sinC，
∵sinC≠0，sin（A+B）=sinC
∴cosC= 
，
又0＜C＜π，
∴C= 
（2）
解：由余弦定理得7=a2+b2﹣2ab ，
∴（a+b）2﹣3ab=7，
∵S= absinC= 
ab= 
，
∴ab=6，
∴（a+b）2﹣18=7，
∴a+b=5，
∴△ABC的周长为5+ 
．
【解析】解三角形.（Ⅰ）已知等式利用正弦定理化简，整理后利用两角和与差的正弦函数公式及诱导公式化简，根据sinC不为0求出cosC的值，即可确定出出C的度数；（2）利用余弦定理列出关系式，利用三角形面积公式列出关系式，求出a+b的值，即可求△ABC的周长.此题考查了正弦、余弦定理，三角形的面积公式，以及三角函数的恒等变形，熟练掌握定理及公式是解本题的关键．
冲刺100分单元优化练考卷系列答案【题目】某公司即将推车一款新型智能手机，为了更好地对产品进行宣传，需预估市民购买该款手机是否与年龄有关，现随机抽取了50名市民进行购买意愿的问卷调查，若得分低于60分，说明购买意愿弱；若得分不低于60分，说明购买意愿强，调查结果用茎叶图表示如图所示.
（1）根据茎叶图中的数据完成
列联表，并判断是否有95%的把握认为市民是否购买该款手机与年龄有关？
购买意愿强 | 购买意愿弱 | 合计 | |
20~40岁 | |||
大于40岁 | |||
合计 |
（2）从购买意愿弱的市民中按年龄进行分层抽样，共抽取5人，从这5人中随机抽取2人进行采访，求这2人都是年龄大于40岁的概率.
附：
.
