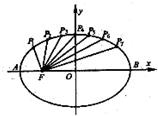
题目内容
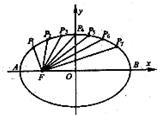 如图把椭圆
如图把椭圆| x2 |
| 25 |
| y2 |
| 16 |
分析:根据椭圆的对称性知,|P1F1|+|P7F1|=|P1F1|+|P1F2|=2a,同理其余两对的和也是2a,又|P4F1|=a,由此可得答案.
解答: 解:如图,把椭圆
解:如图,把椭圆
+
=1的长轴AB分成8等份,
过每个分点作x轴的垂线交椭圆的上半部分于P1,P2,P3,P4,P5,P6,P7七个点,F是椭圆的一个焦点,
则根据椭圆的对称性知,|P1F1|+|P7F1|=|P1F1|+|P1F2|=2a,
同理其余两对的和也是2a,
又|P4F1|=a,
∴|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|+|P7F|
=7a=35,
故答案为35.
 解:如图,把椭圆
解:如图,把椭圆| x2 |
| 25 |
| y2 |
| 16 |
过每个分点作x轴的垂线交椭圆的上半部分于P1,P2,P3,P4,P5,P6,P7七个点,F是椭圆的一个焦点,
则根据椭圆的对称性知,|P1F1|+|P7F1|=|P1F1|+|P1F2|=2a,
同理其余两对的和也是2a,
又|P4F1|=a,
∴|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|+|P7F|
=7a=35,
故答案为35.
点评:作出图象.数形结合,事半成功倍.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
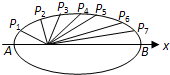 如图,把椭圆
如图,把椭圆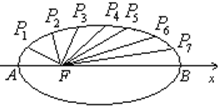 如图,把椭圆
如图,把椭圆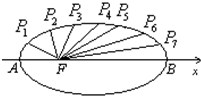 如图,把椭圆
如图,把椭圆