题目内容
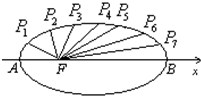 如图,把椭圆
如图,把椭圆| x2 |
| 25 |
| y2 |
| 16 |
| A、40 | B、30 | C、32 | D、35 |
分析:根据题意要求的是焦半径的和因此可利用椭圆的第二定义可得焦半径的通式|PF|=5-
x,所以所求的焦半径的和即可转化为各点横坐标的和,故需根据对称性分析出p4点为椭圆与Y轴正半轴的交点且P1,P2,P3与P5,P6,P7分别关于Y轴对称然后代入化简即可.
| 3 |
| 5 |
解答:解:不妨设P点是椭圆上的任意点则由椭圆的第二定义可得:
=
又a=5,b=4,c=
=3故|PF|=5-
x ①
∵把椭圆
+
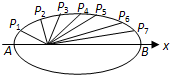
=1的长轴AB分成8等份,过每个分点作x轴的垂线交椭圆的上半部分于P1,P2,P3,P4,P5,P6,P7七个点
∴p4点为椭圆与Y轴正半轴的交点且P1,P2,P3与P5,P6,P7分别关于Y轴对称
∴不妨设p1(x1,y1),p2(x2,y2),p3(x3,y3)且x1<0,x2<0,x3<0,p4(0,4)
∴p5(-x3,y3),p6(-x2,y2),p7(-x1,y1)
∴由①可得|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|+|P7F|=(5+
x1)+(5+
x2)+(5+
x3)+(5-
×0)+ (5-
x3)+(5-
x2)+(5-
x1)
∴|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|+|P7F|=5×7=35
故答案选D
| |PF| | ||
|
| c |
| a |
| a2- b2 |
| 3 |
| 5 |
∵把椭圆
| x2 |
| 25 |
| y2 |
| 16 |
∴p4点为椭圆与Y轴正半轴的交点且P1,P2,P3与P5,P6,P7分别关于Y轴对称
∴不妨设p1(x1,y1),p2(x2,y2),p3(x3,y3)且x1<0,x2<0,x3<0,p4(0,4)
∴p5(-x3,y3),p6(-x2,y2),p7(-x1,y1)
∴由①可得|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|+|P7F|=(5+
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
∴|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|+|P7F|=5×7=35
故答案选D
点评:本题主要考查了利用椭圆的第二定义求椭圆的焦半径的和.解题的关键是要利用椭圆的第二定义可得焦半径的通式|PF|=5-
x再根据对称性得出p4点为椭圆与Y轴正半轴的交点且P1,P2,P3与P5,P6,P7分别关于Y轴对称同时椭圆的准线方程形式:x=
或y=
也要熟记!
| 3 |
| 5 |
| + |
. |
| a2 |
| c |
| + |
. |
| a2 |
| c |

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
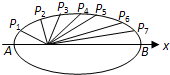 如图,把椭圆
如图,把椭圆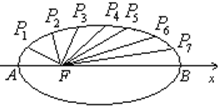 如图,把椭圆
如图,把椭圆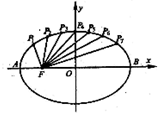 如图,把椭圆
如图,把椭圆