题目内容
设函数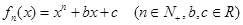
(1)设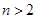 ,
,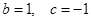 ,证明:
,证明: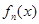 在区间
在区间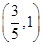 内存在唯一的零点;
内存在唯一的零点;
(2)设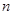 为偶数,
为偶数,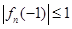 ,
,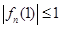 ,求
,求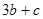 的最小值和最大值;
的最小值和最大值;
(3)设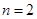 ,若对任意
,若对任意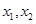
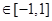 ,有
,有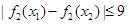 ,求
,求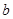 的取值范围;
的取值范围;
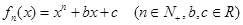
(1)设
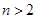 ,
,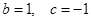 ,证明:
,证明: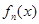 在区间
在区间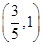 内存在唯一的零点;
内存在唯一的零点;(2)设
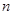 为偶数,
为偶数,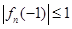 ,
,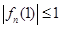 ,求
,求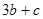 的最小值和最大值;
的最小值和最大值;(3)设
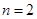 ,若对任意
,若对任意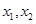
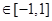 ,有
,有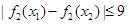 ,求
,求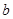 的取值范围;
的取值范围;(1)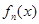 在区间
在区间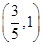 内存在唯一的零点.
内存在唯一的零点.
(2)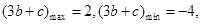 (3)
(3)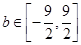 。
。
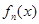 在区间
在区间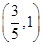 内存在唯一的零点.
内存在唯一的零点.(2)
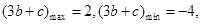 (3)
(3)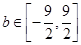 。
。试题分析:(1)由
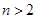 ,
,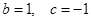 ,得
,得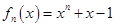
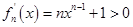 对
对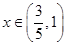 恒成立,从而
恒成立,从而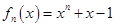 在
在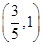 单调递增,
单调递增,又
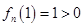 ,
,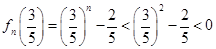 ,
,即
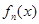 在区间
在区间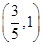 内存在唯一的零点.
内存在唯一的零点. 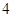 分
分(2)因为
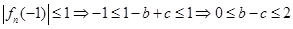
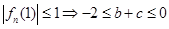 由线性规划
由线性规划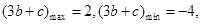
(或
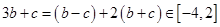 ,
,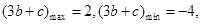 )
) 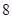 分
分(3)当
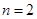 时,
时,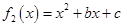
(Ⅰ)当
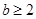 或
或 时,即
时,即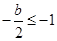 或
或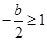 ,此时
,此时只需满足
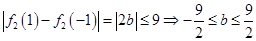 ,从而
,从而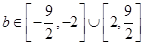
(Ⅱ)当
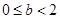 时,即
时,即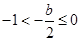 ,此时
,此时只需满足
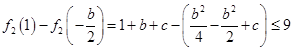 ,即
,即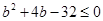
解得:
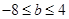 ,从而
,从而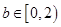
(Ⅲ)当
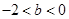 时,即
时,即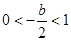 ,此时
,此时只需满足
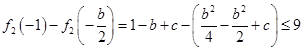 ,即
,即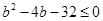
解得:
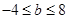 ,从而
,从而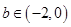
综上所述:
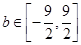
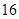 分
分点评:综合题,本题综合性较强,难度较大。确定方程只有一个实根,通过构造函数,研究其单调性实现。由
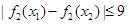 ,确定得到
,确定得到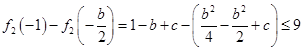 ,进一步得到
,进一步得到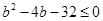 ,求得b的范围。
,求得b的范围。
练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 ,②
,② ,③
,③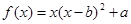 ,(以上三式中
,(以上三式中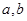 均是不为零的常数,且
均是不为零的常数,且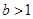 )
)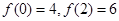 ,求出所选函数
,求出所选函数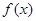 的解析式(注:函数的定义域是
的解析式(注:函数的定义域是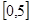 )。其中
)。其中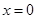 表示8月1日,
表示8月1日, 表示9月1日,……,以此类推;为保证该地的经济收益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该西红柿将在哪几个月份内价格下跌。
表示9月1日,……,以此类推;为保证该地的经济收益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该西红柿将在哪几个月份内价格下跌。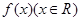 满足:任意的
满足:任意的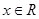 ,都有
,都有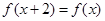 ,且
,且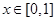 时,
时,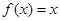 ,则函数
,则函数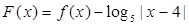 的所有零点之和为 .
的所有零点之和为 . 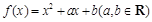 ,
,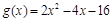 ,且
,且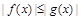 对
对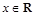 恒成立.
恒成立.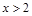 ,不等式
,不等式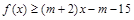 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.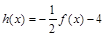 ,那么当
,那么当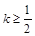 时,是否存在区间
时,是否存在区间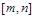 (
(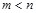 ),使得函数
),使得函数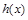 在区间
在区间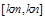 ?若存在,请求出区间
?若存在,请求出区间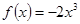 的图象
的图象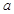 元(
元(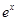 (e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。
(e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。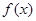 在
在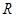 上满足
上满足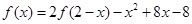 ,则曲线
,则曲线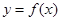 在点
在点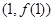 处的切线方程是__________.
处的切线方程是__________.
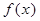
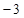


 ( )
( )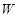 与它的航行速度
与它的航行速度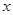 (公里/小时)的函数关系式;
(公里/小时)的函数关系式;