题目内容
命题“若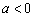 ,则一元二次方程
,则一元二次方程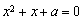 有实根”的原命题与其逆命题、否命题、逆否命题中真命题的个数是( )
有实根”的原命题与其逆命题、否命题、逆否命题中真命题的个数是( )
A.0 B.2 C.4 D.不确定
【答案】
B
【解析】
试卷分析:原命题为:“若a<0,则方程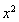 +x+a=0有实根”,因为方程的判别式为△=1-4a,∴a<0时,△>0,∴方程
+x+a=0有实根”,因为方程的判别式为△=1-4a,∴a<0时,△>0,∴方程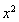 +x+a=0有实根,故命题为真;
+x+a=0有实根,故命题为真;
逆否命题为:“若方程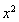 +x+a=0没有实根,则m≥0”,根据原命题与逆否命题,真假一致,可知命题为真;逆命题为:“若方程
+x+a=0没有实根,则m≥0”,根据原命题与逆否命题,真假一致,可知命题为真;逆命题为:“若方程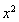 +x+a=0有实根,则m<0”,因为方程有实根,所以判别式△=1-4m≥0,∴m≤
+x+a=0有实根,则m<0”,因为方程有实根,所以判别式△=1-4m≥0,∴m≤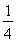 ,显然m<0不一定成立,故命题为假;
,显然m<0不一定成立,故命题为假;
否命题为:“若m≥0,则方程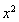 +x+a=0没有实根”,根据否命题与逆命题,真假一致,可知命题为假;故正确的命题有2个;
+x+a=0没有实根”,根据否命题与逆命题,真假一致,可知命题为假;故正确的命题有2个;
故答案为:B.
考点:四种命题的真假关系.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 ”是“一元二次不等式ax2+bx+c≥0的解集为R的充要条件
”是“一元二次不等式ax2+bx+c≥0的解集为R的充要条件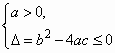 ”是“一元二次不等式ax2+bc+c≥0的解集为R的充要条件
”是“一元二次不等式ax2+bc+c≥0的解集为R的充要条件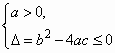 ”是“一元二次不等式ax2+bx+c≥0的解集为R的充要条件
”是“一元二次不等式ax2+bx+c≥0的解集为R的充要条件