题目内容
设各项均为正数的数列
的前
项和为
，满足
且
构成等比数列．
(1) 证明：
；
(2) 求数列的通项公式；
(3) 证明：对一切正整数，有
．
【解析】（1）当
时，
，
（2）当
时，
，
,
当时，是公差
的等差数列.
构成等比数列，
，
，解得
,
由（1）可知，
是首项
,公差的等差数列.
数列的通项公式为
.
（3）
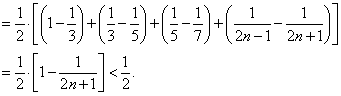
【解析】本题考查很常规，第（1）（2）两问是已知求
，是等差数列，第（3）问只需裂项求和即可，估计不少学生猜出通项公式，跳过第（2）问，作出第（3）问.本题易错点在分成，来做后，不会求
，没有证明也满足通项公式.
练习册系列答案
相关题目