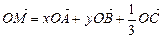题目内容
已知棱长为1的正方体AC1,E、F分别是B1C1、C1D的中点.
(1)求点A1到平面的BDEF的距离;
(2)求直线A1D与平面BDEF所成的角.
(1)点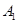 到平面的BDEF的距离;(2)直线A1D与平面BDEF所成的角为
到平面的BDEF的距离;(2)直线A1D与平面BDEF所成的角为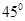 .
.
解析试题分析:(1)建立空间坐标系,分别写出各点的坐标,设点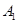 在平面BDEF上的射影为H,连结A1D,知A1D是平面BDEF的斜线段;求出
在平面BDEF上的射影为H,连结A1D,知A1D是平面BDEF的斜线段;求出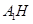 的长即为点
的长即为点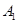 到平面的BDEF的距离;
到平面的BDEF的距离;
(2)由(1)可知,△ 为等腰直角三角形,
为等腰直角三角形, 即直线A1D与平面BDEF所成的角.
即直线A1D与平面BDEF所成的角.
(1)如图,建立空间直角坐标系D—xyz,
则知B(1,1,0),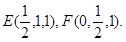
设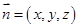 是平面
是平面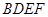 的法向量,
的法向量,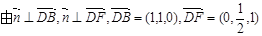
得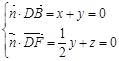 则
则
令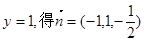 .
.
设点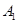 在平面BDEF上的射影为H,连结A1D,知A1D是平面BDEF的斜线段.
在平面BDEF上的射影为H,连结A1D,知A1D是平面BDEF的斜线段.

即点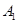 到平面BDEF的距离为1.
到平面BDEF的距离为1.
(2)由(1)知,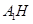 =1,又A1D=
=1,又A1D=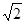 ,则△
,则△ 为等腰直角三角形,
为等腰直角三角形,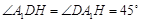
考点:空间距离、空间角的求法.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
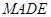 的边长为2,
的边长为2, ,
, 分别为
分别为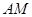 ,
,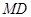 的中点,在五棱锥
的中点,在五棱锥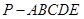 中,
中,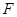 为棱
为棱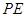 的中点,平面
的中点,平面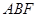 与棱
与棱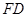 ,
,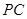 分别交于
分别交于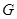 ,
,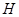 .
.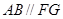 ;
;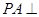 底面
底面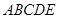 ,且
,且 ,求直线
,求直线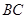 与平面
与平面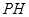 的长.
的长.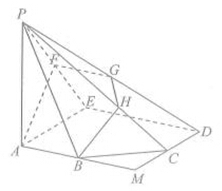
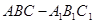 中,
中,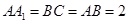 ,
,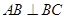 。M、N分别是AC和BB1的中点。
。M、N分别是AC和BB1的中点。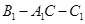 的大小。
的大小。 ⊥平面
⊥平面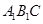 ,
,  的长度。
的长度。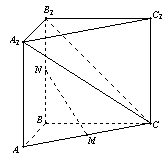
 平面
平面 ,
, ∥
∥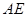 ,
,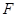 是
是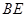 的中点,
的中点,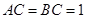 ,
,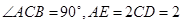 .
.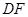 ∥平面
∥平面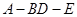 的大小的余弦值.
的大小的余弦值.
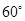 ,∠BAC
,∠BAC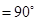 ,AD是BC上的高,沿AD把△ABD折起,使∠BDC
,AD是BC上的高,沿AD把△ABD折起,使∠BDC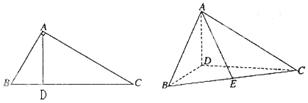
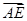 与
与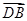 夹角的余弦值.
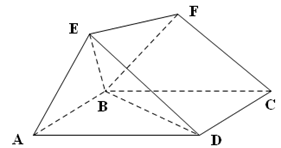
夹角的余弦值. 是边长为2的菱形,且
是边长为2的菱形,且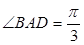 ,以
,以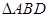 与
与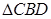 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥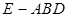 与
与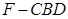 ,且
,且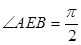 .
.
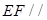 平面
平面 与平面
与平面 所成锐角二面角的余弦值.
所成锐角二面角的余弦值. ,点M,N分别在线段PA和BD上,BN=
,点M,N分别在线段PA和BD上,BN= BD.
BD. ,求线段MN的长度.
,求线段MN的长度.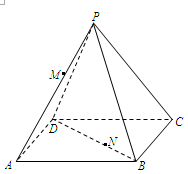
 ,b=
,b= .
.