题目内容
如图,正方体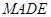 的边长为2,
的边长为2, ,
, 分别为
分别为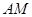 ,
,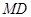 的中点,在五棱锥
的中点,在五棱锥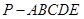 中,
中,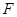 为棱
为棱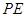 的中点,平面
的中点,平面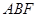 与棱
与棱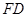 ,
,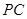 分别交于
分别交于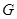 ,
,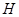 .
.
(1)求证: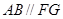 ;
;
(2)若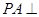 底面
底面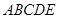 ,且
,且 ,求直线
,求直线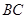 与平面
与平面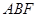 所成角的大小,并求线段
所成角的大小,并求线段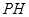 的长.
的长.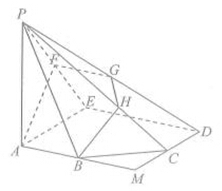
(1)详见解析;(2)2.
解析试题分析:(1)利用正方形的性质,证明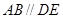 ,利用线面平行的判定定理证明
,利用线面平行的判定定理证明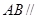 平面
平面 ,再用线面平行的性质定理证明
,再用线面平行的性质定理证明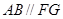 ;(2)由条件
;(2)由条件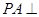 底面
底面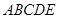 ,证明
,证明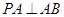 ,
, ,
,
建立空间直角坐标系 ,利用向量法求解,先求平面
,利用向量法求解,先求平面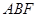 的法向量,利用公式
的法向量,利用公式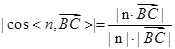 ,求直线
,求直线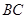 与平面
与平面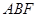 所成的角,再设点
所成的角,再设点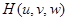 ,因为点
,因为点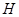 在棱
在棱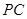 上,所以可设
上,所以可设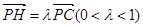 ,利用向量的坐标运算,求
,利用向量的坐标运算,求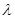 的值,最后用空间中两点间的距离公式求
的值,最后用空间中两点间的距离公式求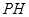 .
.
(1)在正方形 中,因为
中,因为 是
是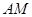 的中点,所以
的中点,所以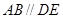 ,
,
因为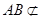 平面
平面 ,所以
,所以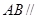 平面
平面 ,
,
因为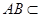 平面
平面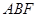 ,且平面
,且平面 平面
平面
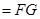 ,
,
所以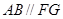 .
.
(2)因为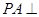 底面
底面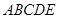 ,所以
,所以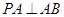 ,
, ,
,
如图建立空间直角坐标系 ,则
,则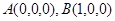 ,
,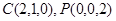 ,
,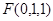 ,
,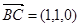 ,设平面
,设平面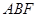 的法向量为
的法向量为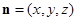 ,
,
则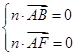 ,即
,即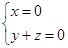 ,令
,令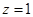 ,则
,则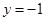 ,所以
,所以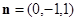 ,
,
设直线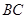 与平面
与平面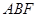 所成的角为
所成的角为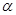 ,则
,则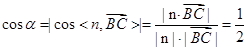 ,
,
因此直线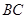 与平面
与平面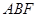 所成的角为
所成的角为 ,
,
设点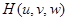 ,因为点
,因为点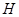 在棱
在棱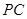 上,所以可设
上,所以可设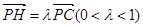 ,
,
即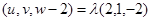 ,所以
,所以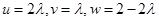 ,
,
因为向量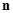 是平面
是平面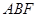 的法向量,所以
的法向量,所以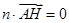 ,
,
即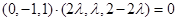 ,解得
,解得
练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
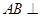 侧面
侧面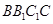 ,AB=BC=1,BB1=2,∠BCC1=
,AB=BC=1,BB1=2,∠BCC1= .
.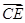 =l
=l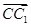 (0≤l≤1),且平面AB1E与BB1E所成的锐二面角
(0≤l≤1),且平面AB1E与BB1E所成的锐二面角 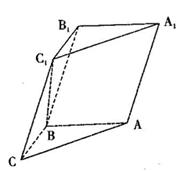
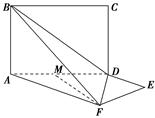
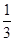 ,求AB的长.
,求AB的长.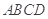 是正方形,
是正方形,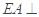 平面
平面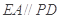 ,
,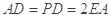 ,
,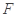 ,
,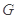 ,
, 分别为
分别为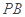 ,
,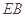 ,
,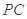 的中点.
的中点.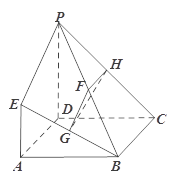
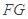
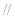 平面
平面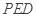 ;
;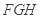 与平面
与平面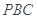 所成锐二面角的大小.
所成锐二面角的大小.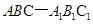 ,
,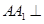 平面
平面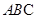 ,
,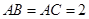 ,
,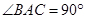 ,四边形
,四边形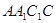 为正方形,
为正方形,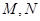 分别为
分别为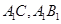 中点.
中点.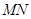 ∥面
∥面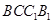 ;
; —
—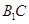 —
—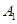 的余弦值.
的余弦值.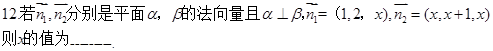
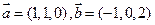 ,若向量
,若向量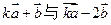 互相垂直,则
互相垂直,则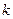 的值为 。
的值为 。 ,求三棱锥E-ACD的体积.
,求三棱锥E-ACD的体积.