题目内容
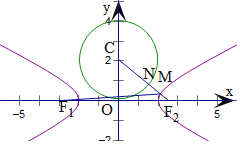
【题目】已知双曲线
的左、右焦点分别为
，实轴长为4，渐近线方程为
，点N在圆
上，则
的最小值为( )
A. 
B. 5C. 6D. 7
【答案】B
【解析】
求得双曲线的a，b，可得双曲线方程，求得焦点坐标，运用双曲线的定义和三点共线取得最小值，连接CF2，交双曲线于M，圆于N，计算可得所求最小值．
由题意可得2a＝4，即a＝2，
渐近线方程为y＝±
x，即有
，
即b＝1，可得双曲线方程为
y2＝1，
焦点为F1（
，0），F2，（
，0），
由双曲线的定义可得|MF1|＝2a+|MF2|＝4+|MF2|，
由圆x2+y2﹣4y＝0可得圆心C（0，2），半径r＝2，
|MN|+|MF1|＝4+|MN|+|MF2|，
连接CF2，交双曲线于M，圆于N，
可得|MN|+|MF2|取得最小值，且为|CF2|
3，
则则|MN|+|MF1|的最小值为4+3﹣2＝5．
故选：B．
【题目】空气质量指数PM2.5（单位：μg/m3）表示每立方米空气中可入肺颗粒物的含量，这个值越高，就代表空气污染越严重：
日均浓度 |
|
|
|
|
|
|
空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲、乙两城市2013年2月份中的15天对空气质量指数PM2.5进行监测，获得PM2.5日均浓度指数数据如茎叶图所示：
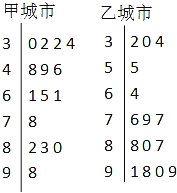
（Ⅰ）根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好？（注：不需说明理由）
（Ⅱ）在15天内任取1天，估计甲、乙两城市空气质量类别均为优或良的概率；
（Ⅲ）在乙城市15个监测数据中任取2个，设X为空气质量类别为优或良的天数，求X的分布列及数学期望．
【题目】为了解某地区初中学生的体质健康情况,统计了该地区8所学校学生的体质健康数据,按总分评定等级为优秀,良好,及格,不及格.良好及其以上的比例之和超过40%的学校为先进校.各等级学生人数占该校学生总人数的比例如下表:
比例 学校 等级 | 学校A | 学校B | 学校C | 学校D | 学校E | 学校F | 学校G | 学校H |
优秀 | 8% | 3% | 2% | 9% | 1% | 22% | 2% | 3% |
良好 | 37% | 50% | 23% | 30% | 45% | 46% | 37% | 35% |
及格 | 22% | 30% | 33% | 26% | 22% | 17% | 23% | 38% |
不及格 | 33% | 17% | 42% | 35% | 32% | 15% | 38% | 24% |
(1)从8所学校中随机选出一所学校,求该校为先进校的概率；
(2)从8所学校中随机选出两所学校,记这两所学校中不及格比例低于30%的学校个数为X,求X的分布列；
(3)设8所学校优秀比例的方差为S12,良好及其以下比例之和的方差为S22,比较S12与S22的大小.(只写出结果)
