题目内容
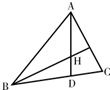 如图所示在△ABC中,sin2A+sin2C=sin2B+sinA.sinC
如图所示在△ABC中,sin2A+sin2C=sin2B+sinA.sinC(1)求B的度数.
(2)设H为△ABC的垂心,且
| BH |
| BC |
分析:(1)根据正弦定理化简已知的等式得到一个关系式,记作①,然后利用余弦定理表示出cosC,把①代入即可求出cosB的值,然后由C的范围,利用特殊角的三角函数值即可求出B的度数;
(2)根据H为△ABC的垂心,把
•
=6转化成
ac,然后利用b2=a2+c2-ac≥2ac-ac,求出b的最小值.
(2)根据H为△ABC的垂心,把
| BH |
| BC |
| 1 |
| 2 |
解答:解:(1)由sin2A+sin2C=sin2B+sinA.sinC,
利用正弦定理化简得:a2+c2=b2+ac,①
则根据余弦定理得:cosB=
∴cosB=
,由B∈(0,180°),
得到:B=60°;
(2)6=
•
=/
/•/
/•cos∠CBH=/
/•/
/=
/
/•/
/=
ac
∴ac=12
∴b2=a2+c2-ac≥2ac-ac=ac=12
∴bmin=2
利用正弦定理化简得:a2+c2=b2+ac,①
则根据余弦定理得:cosB=
| a2+c2-b2 |
| 2ac |
∴cosB=
| 1 |
| 2 |
得到:B=60°;
(2)6=
| BH |
| BC |
| BH |
| BC |
| BD |
| BC |
| 1 |
| 2 |
| AB |
| BC |
| 1 |
| 2 |
∴ac=12
∴b2=a2+c2-ac≥2ac-ac=ac=12
∴bmin=2
| 3 |
点评:本题考查了正弦定理、余弦定理以及求最值解决数学问题,解本题的关键是利用正弦定理化简已知的等式,综合性比较强,要求学生掌握知识全面.

练习册系列答案
相关题目
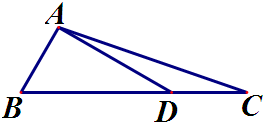 如图所示在△ABC中,D在边BC上,且BD=2,DC=1,∠B=60°,∠ADB=30°,求AC的长及△ABC的面积.
如图所示在△ABC中,D在边BC上,且BD=2,DC=1,∠B=60°,∠ADB=30°,求AC的长及△ABC的面积.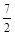 ,
求边长a.
,
求边长a.