题目内容
如图所示,在△ABC中,已知BC=15,AB∶AC=7∶8,sinB=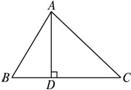
思路分析:由已知设AB=7x,AC=8x,因此要求AD的长只需求出x.△ABC中已知三边只需再有一个角,根据余弦定理便可求出x,而用正弦定理恰好求角C.
解:在△ABC中,由已知设AB=7x,AC=8x,
由正弦定理得![]() =
=![]() ,
,
∴sinC=![]() =
=![]() ×
×![]() =
=![]() .
.
∴C=60°(C=120°舍去,否则由8x>7x,知B也为钝角,不合要求).
再由余弦定理得
(7x)2=(8x)2+152-2×8x×15cos60°,
∴x2-8x+15=0.
∴x=3,或x=5.
∴AB=21,或AB=35.
在△ABD中,AD=ABsinB=![]() AB,
AB,
∴AD=12![]() ,或AD=20
,或AD=20![]() .
.

练习册系列答案
相关题目
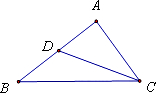 如图所示,在△ABC中,点D是边AB的中点,则向量
如图所示,在△ABC中,点D是边AB的中点,则向量| DC |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
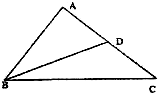 如图所示,在△ABC,已知
如图所示,在△ABC,已知 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD= 如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则
如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=