题目内容
设函数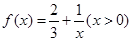 ,数列
,数列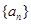 满足
满足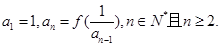
(1)求数列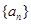 的通项公式;
的通项公式;
(2)对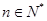 ,设
,设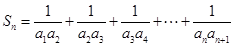 ,若
,若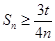 恒成立,求实数
恒成立,求实数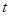 的取值范围.
的取值范围.
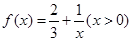 ,数列
,数列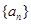 满足
满足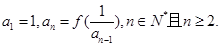
(1)求数列
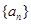 的通项公式;
的通项公式;(2)对
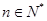 ,设
,设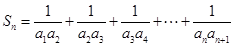 ,若
,若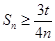 恒成立,求实数
恒成立,求实数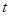 的取值范围.
的取值范围.(1) 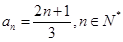 .(2)
.(2)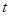 的取值范围是
的取值范围是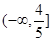 .
.
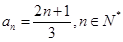 .(2)
.(2)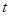 的取值范围是
的取值范围是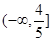 .
.试题分析:(1)由
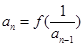 可得:
可得: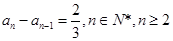 .所以这是一个等差数列,由等差数列的通项公式即可得.(2)
.所以这是一个等差数列,由等差数列的通项公式即可得.(2) ,
,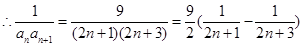 .这是典型的用裂项法求和的数列. 由
.这是典型的用裂项法求和的数列. 由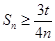 得
得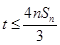 .要使得
.要使得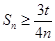 恒成立,则
恒成立,则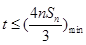 .用裂项法可求得
.用裂项法可求得 ,从而得
,从而得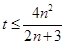 ,令
,令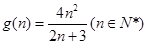 .下面求
.下面求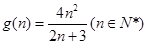 的最小值.将
的最小值.将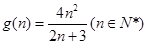 变形得
变形得 .利用函数
.利用函数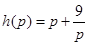 的单调性便可得
的单调性便可得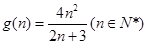 最小值,进而得
最小值,进而得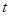 的取值范围.
的取值范围.试题解析:(1)由
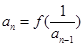 可得:
可得: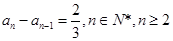 .
.所以
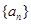 是等差数列.
是等差数列.又因为
 .
.(2)
 .
. ,
,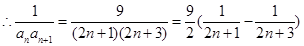 .
. .
. 恒成立.
恒成立.令
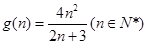 .
. .
.令
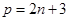 ,则
,则 .
.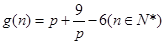 ,易知
,易知 时,
时,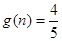 最小.
最小.所以
 ,即
,即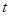 的取值范围是
的取值范围是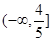 .
.
练习册系列答案
相关题目
 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列 的一个是等比数列的子列;
的一个是等比数列的子列; ,公比为
,公比为 .求证:当
.求证:当 时,数列
时,数列 是等差数列,且
是等差数列,且 .
. ,求数列
,求数列 的前
的前 项和.
项和.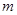 的有穷数列数集
的有穷数列数集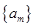 ,记
,记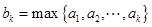
 ,即
,即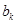 为
为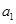 、
、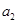 、
、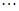 、
、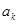 中的最大值,并称数列
中的最大值,并称数列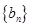 是
是 的控制数列.如
的控制数列.如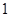 、
、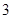 、
、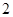 、
、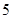 、
、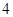 、
、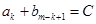 (
(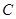 为常数,
为常数,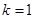 、
、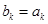
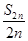 =2013,求n的值;
=2013,求n的值;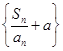 是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+
是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+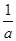 .
.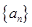 中,
中,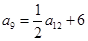 ,则数列
,则数列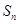 表示数列
表示数列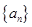 的前
的前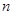 项和,若对任意的
项和,若对任意的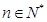 满足
满足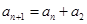 ,且
,且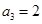 ,则
,则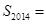 ( )
( )


