Question

若关于x的方程x²-(a²+b²-6b)x+a²+b²+2a-4b+1＝0的两个实数根x₁,x₂满足x₁≤0≤x₂≤1,则a²+b²+4a+4的最小值和最大值分别为

A.和＋2                                B.和9+4

C.和16                                      D.1和9-4

Answer 1

解析：令f(x)=x²-(a²+b²-6b)x+a²+b²+2a-4b+1,

∵x₁≤0≤x₂≤1,

∴

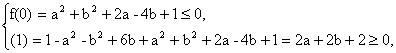
即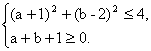

如图可行域为阴影部分,交点为A、B,

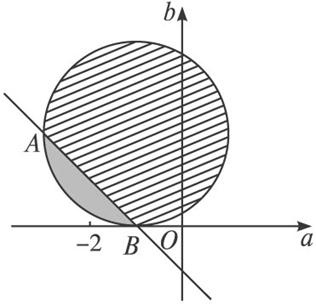
又a²+b²+4a+4=(a+2)²+b²,几何意义为(a,b)与(-2,0)两点间的距离的平方.

∴最小值为,

最大值为=9+.故选B.