题目内容
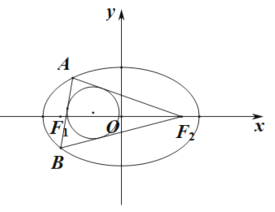
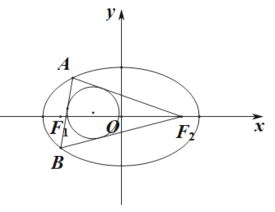
【题目】如图,设椭圆![]() 1的左右焦点分别为F1、F2,过焦点F1的直线交椭圆于A、B两点,若△ABF2的内切圆的面积为4,设A、B两点的坐标分别为A(x1,y1),B(x2,y2),则|y1﹣y2|值为_____.
1的左右焦点分别为F1、F2,过焦点F1的直线交椭圆于A、B两点,若△ABF2的内切圆的面积为4,设A、B两点的坐标分别为A(x1,y1),B(x2,y2),则|y1﹣y2|值为_____.
【答案】![]() .
.
【解析】
根据椭圆方程求得![]() 、
、![]() 的值,从而得到椭圆的焦点坐标.利用椭圆的定义算出
的值,从而得到椭圆的焦点坐标.利用椭圆的定义算出![]() 的周长为16,由圆面积公式求得
的周长为16,由圆面积公式求得![]() 的内切圆半径
的内切圆半径![]() ,从而算出
,从而算出![]() 的面积.最后根据
的面积.最后根据![]() 的形状,算出其面积
的形状,算出其面积![]() ,由此建立关系式并解之,即可得出
,由此建立关系式并解之,即可得出![]() 的值.
的值.
∵椭圆中,a2=16且b2=4,
∴a=4,b=2,c![]() 2
2![]() ,
,
可得椭圆的焦点分别为F1(﹣2![]() ,0)、F2(2
,0)、F2(2![]() ,0),
,0),
设△ABF2的内切圆半径为r,
∵△ABF2的内切圆面积为S=πr2=4,∴r![]() ,
,
根据椭圆的定义,得|AB|+|AF2|+|BF2|=(|AF1|+|AF2|)+(|BF1|+|BF2|)=4a=16.
∴△ABF2的面积S![]() (|AB|+|AF2|+|BF2|)×r
(|AB|+|AF2|+|BF2|)×r![]() 16
16![]() ,
,
又∵△ABF2的面积S=S△AF1F2+S△BF1F2![]() |y1|×|F1F2|
|y1|×|F1F2|![]() |y2|×|F1F2|
|y2|×|F1F2|
![]() (|y1|+|y2|)×|F1F2|=2
(|y1|+|y2|)×|F1F2|=2![]() |y2﹣y1|(A、B在x轴的两侧),
|y2﹣y1|(A、B在x轴的两侧),
∴2![]() |y2﹣y1|
|y2﹣y1|![]() ,解之得|y2﹣y1|
,解之得|y2﹣y1|![]() .
.

练习册系列答案
相关题目