题目内容
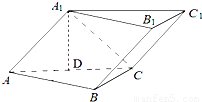
如图,已知斜三棱柱(侧棱不垂直于底面)ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,BC=2,AC=2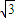 ,AB=2
,AB=2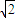 ,AA1=A1C=
,AA1=A1C=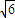 .
.(Ⅰ) 求侧棱B1B在平面A1ACC1上的正投影的长度.
(Ⅱ) 设AC的中点为D,证明A1D⊥底面ABC;
(Ⅲ) 求侧面A1ABB1与底面ABC所成二面角的余弦值.
【答案】分析:(Ⅰ)由B1B∥平面A1ACC1,可得侧棱B1B在平面A1ACC1上的正投影的长度等于侧棱B1B的长度;
(Ⅱ)利用平面A1ACC1⊥平面ABC,可证A1D⊥底面ABC;
(Ⅲ)要求侧面A1ABB1与底面ABC所成二面角的大小,利用三垂线定理作出角,即作DE⊥AB,垂足为E,连A1E,则由A1D⊥面ABC,得A1E⊥AB.所以∠A1ED是面A1ABB1与面ABC所成二面角的平面角,求解即可.
解答: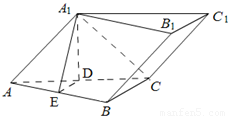 (Ⅰ)解:∵ABC-A1B1C1是斜三棱柱,∴B1B∥平面A1ACC1,
(Ⅰ)解:∵ABC-A1B1C1是斜三棱柱,∴B1B∥平面A1ACC1,
故侧棱B1B在平面A1ACC1上的正投影的长度等于侧棱B1B的长度.(2分)
又BB1=AA1=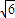 ,故侧棱B1B在平面A1ACC1的正投影的长度等于
,故侧棱B1B在平面A1ACC1的正投影的长度等于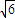 .(3分)
.(3分)
(Ⅱ)证明:∵AC=2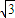 ,AA1=A1C=
,AA1=A1C=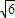 ,∴AC2=AA12+AC12,
,∴AC2=AA12+AC12,
∴△AA1C是等腰直角三角形,(5分)
又D是斜边AC的中点,∴A1D⊥AC(6分)
∵平面A1ACC1⊥平面ABC,∴A1D⊥底面ABC(7分)
(Ⅲ)解:作DE⊥AB,垂足为E,连A1E,
∵A1D⊥面ABC,AB?面ABC,∴A1D⊥AB,
∵A1D∩DE=D,∴AB⊥平面A1ED,(8分)
从而有A1E⊥AB,∴∠A1ED是面A1ABB1与面ABC所成二面角的平面角. (9分)
∵BC=2,AC=2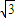 ,AB=2
,AB=2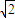 ,∴AC2=BC2+AB2,
,∴AC2=BC2+AB2,
∴△ABC是直角三角形,AB⊥BC
∴ED∥BC,
又D是AC的中点,BC=2,AC=2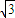 ,∴DE=1,A1D=AD=
,∴DE=1,A1D=AD=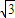 ,
,
∴A1E=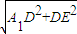 =2
=2
∴cos∠A1ED= =
= ,即侧面A1ABB1与底面ABC所成二面角的余弦值为
,即侧面A1ABB1与底面ABC所成二面角的余弦值为 .(14分)
.(14分)
点评:本题考查面面垂直,考查线面垂直,考查面面角,考查学生分析解决问题的能力,属于中档题.
(Ⅱ)利用平面A1ACC1⊥平面ABC,可证A1D⊥底面ABC;
(Ⅲ)要求侧面A1ABB1与底面ABC所成二面角的大小,利用三垂线定理作出角,即作DE⊥AB,垂足为E,连A1E,则由A1D⊥面ABC,得A1E⊥AB.所以∠A1ED是面A1ABB1与面ABC所成二面角的平面角,求解即可.
解答:
 (Ⅰ)解:∵ABC-A1B1C1是斜三棱柱,∴B1B∥平面A1ACC1,
(Ⅰ)解:∵ABC-A1B1C1是斜三棱柱,∴B1B∥平面A1ACC1,故侧棱B1B在平面A1ACC1上的正投影的长度等于侧棱B1B的长度.(2分)
又BB1=AA1=
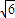 ,故侧棱B1B在平面A1ACC1的正投影的长度等于
,故侧棱B1B在平面A1ACC1的正投影的长度等于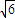 .(3分)
.(3分)(Ⅱ)证明:∵AC=2
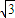 ,AA1=A1C=
,AA1=A1C=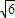 ,∴AC2=AA12+AC12,
,∴AC2=AA12+AC12,∴△AA1C是等腰直角三角形,(5分)
又D是斜边AC的中点,∴A1D⊥AC(6分)
∵平面A1ACC1⊥平面ABC,∴A1D⊥底面ABC(7分)
(Ⅲ)解:作DE⊥AB,垂足为E,连A1E,
∵A1D⊥面ABC,AB?面ABC,∴A1D⊥AB,
∵A1D∩DE=D,∴AB⊥平面A1ED,(8分)
从而有A1E⊥AB,∴∠A1ED是面A1ABB1与面ABC所成二面角的平面角. (9分)
∵BC=2,AC=2
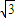 ,AB=2
,AB=2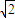 ,∴AC2=BC2+AB2,
,∴AC2=BC2+AB2,∴△ABC是直角三角形,AB⊥BC
∴ED∥BC,
又D是AC的中点,BC=2,AC=2
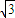 ,∴DE=1,A1D=AD=
,∴DE=1,A1D=AD=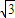 ,
,∴A1E=
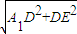 =2
=2∴cos∠A1ED=
 =
= ,即侧面A1ABB1与底面ABC所成二面角的余弦值为
,即侧面A1ABB1与底面ABC所成二面角的余弦值为 .(14分)
.(14分)点评:本题考查面面垂直,考查线面垂直,考查面面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 (甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=
(甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC= 如图,已知斜三棱柱ABC-A1B1C1中,AB=AC,D为BC的中点.
如图,已知斜三棱柱ABC-A1B1C1中,AB=AC,D为BC的中点.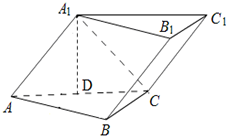 如图,已知斜三棱柱(侧棱不垂直于底面)ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,
如图,已知斜三棱柱(侧棱不垂直于底面)ABC-A1B1C1的侧面A1ACC1与底面ABC垂直, 如图,已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,且BA1⊥AC1.
如图,已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,且BA1⊥AC1.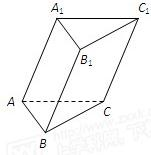 如图,已知斜三棱柱ABC-A1B1C1的底面边长分别是AB=AC=10cm,BC=12cm,侧棱AA1=13cm,顶点A1与下底面各个顶点的距离相等,求这个棱柱的全面积.
如图,已知斜三棱柱ABC-A1B1C1的底面边长分别是AB=AC=10cm,BC=12cm,侧棱AA1=13cm,顶点A1与下底面各个顶点的距离相等,求这个棱柱的全面积.