题目内容
观察以下等式:
sin230°+cos260°+sin 30°·cos 60°= ,
,
sin240°+cos270°+sin 40°·cos 70°= ,
,
sin215°+cos245°+sin 15°·cos 45°= .
.
…
写出反映一般规律的等式,并给予证明.
sin230°+cos260°+sin 30°·cos 60°=
 ,
,sin240°+cos270°+sin 40°·cos 70°=
 ,
,sin215°+cos245°+sin 15°·cos 45°=
 .
.…
写出反映一般规律的等式,并给予证明.
sin2α+cos2(α+30°)+ sin α·cos(α+30°)=

反映一般规律的等式是(表述形式不唯一):
sin2α+cos2(α+30°)+ sin α·cos(α+30°)= .
.
证明如下:
sin2α+cos2(α+30°)+sin α·cos(α+30°)
=sin2α+(cos α·cos 30°-sin α·sin 30°)2
+sin α·(cos αcos 30°-sin α·sin 30°)
=sin2α+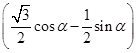 2+
2+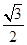 sin α ·cos α-
sin α ·cos α-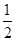 sin2α
sin2α
=sin2α+ cos2α+
cos2α+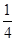 sin2α-
sin2α-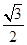 sin α·cos α+
sin α·cos α+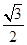 sin α·cos α-
sin α·cos α-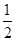 sin2α=
sin2α= (sin2α+cos2α)=
(sin2α+cos2α)= .
.
sin2α+cos2(α+30°)+ sin α·cos(α+30°)=
 .
.证明如下:
sin2α+cos2(α+30°)+sin α·cos(α+30°)
=sin2α+(cos α·cos 30°-sin α·sin 30°)2
+sin α·(cos αcos 30°-sin α·sin 30°)
=sin2α+
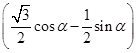 2+
2+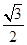 sin α ·cos α-
sin α ·cos α-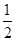 sin2α
sin2α=sin2α+
 cos2α+
cos2α+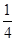 sin2α-
sin2α-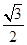 sin α·cos α+
sin α·cos α+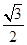 sin α·cos α-
sin α·cos α-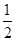 sin2α=
sin2α= (sin2α+cos2α)=
(sin2α+cos2α)= .
.
练习册系列答案
相关题目
 ,则
,则 ”类推出“若
”类推出“若 ,则
,则 ”类推出“
”类推出“ ”
” (
( )”
)” ” 类推出“
” 类推出“ ”
” =1,若以a、b、c为三边构造三角形,则c的取值范围是________.
=1,若以a、b、c为三边构造三角形,则c的取值范围是________. ,把这个结论类比到空间:在三棱锥A-BCD中(如图所示),平面DEC平分二面角A-CD-B且与AB相交于E,则得到的类比的结论是________.
,把这个结论类比到空间:在三棱锥A-BCD中(如图所示),平面DEC平分二面角A-CD-B且与AB相交于E,则得到的类比的结论是________.
 +…+
+…+ ,写出S1,S2,S3,S4的值,归纳并猜想出结果,并给出证明.
,写出S1,S2,S3,S4的值,归纳并猜想出结果,并给出证明.
 ,
, ,
, ,
,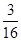

 排在数表的第n行,第m列,则m+n=___________。
排在数表的第n行,第m列,则m+n=___________。















 ,则( ).
,则( ).
