题目内容
(本小题满分12分)一个口袋内装有形状、大小相同的2个白球和3个黑球。
(1)从中随机地摸出一个球不放回,再随机地摸出一个球,求两球同时是黑球的概率;
(2)从中随机地摸出一个球,放回后再随机地摸出一个球,求两球颜色恰好不同的概率
解:设2个白球的编号为1、2;3个黑球的编号为3、4、5。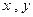 分别表示第一次、第二
分别表示第一次、第二 次取球的编号,则记号
次取球的编号,则记号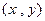 表示两次取球的结果。所有的结果列表如下:
表示两次取球的结果。所有的结果列表如下: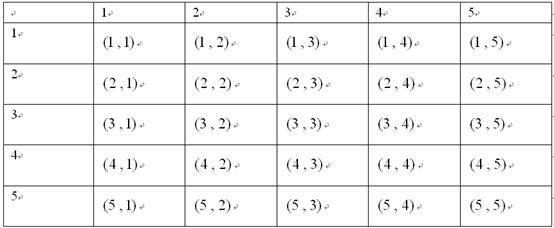
(1)设事件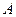 =从中随机地摸出一个球不放回,再随机地摸出一个球,两球同时是黑球。由表可知,所有等可能的取法有20种,事件
=从中随机地摸出一个球不放回,再随机地摸出一个球,两球同时是黑球。由表可知,所有等可能的取法有20种,事件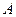 包含
包含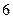 种,
种,
所以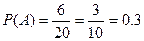 ……6分
……6分
(2)设事件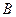 =从中随机地摸出一个球,放回后再随机地摸出一个球,两球恰好颜色不同。由表可知,所以等可能的取法有25种,事件
=从中随机地摸出一个球,放回后再随机地摸出一个球,两球恰好颜色不同。由表可知,所以等可能的取法有25种,事件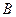 包含12种,
包含12种,
所以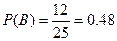 …12分
…12分
解析

练习册系列答案
相关题目
有六种不同颜色,给如图的六个区域涂色,要求相邻区域不同色,不同的涂色方法共有( )
| A.4320 | B.2880 | C.1440 | D.720 |
阅读右面的程序框图,运行相应的程序,输出的结果为( )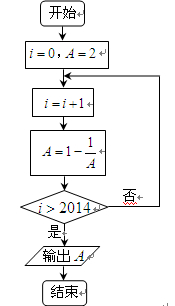
A.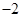 | B.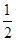 | C.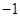 | D.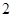 |
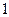 个白球和
个白球和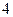 个黑球,每次从中任取
个黑球,每次从中任取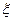 的分布列,并求
的分布列,并求 出
出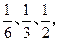 若在一段时间内打进三个电话,
若在一段时间内打进三个电话, 概率
概率