题目内容
已知盒中装有仅颜色不同的玻璃球6个,其中红球2个、黑球3个、白球1个.
(1)从中任取1个球, 求取得红球或黑球的概率;
(2)从中一次取2个不同的球,试列出所有基本事件;并求至少有一个是红球概率。
(3)从中取2次,每次取1个球,在放回的条件下求至少有一个是红球概率。
解:(1) .(2)
.(2) 。(3)P
。(3)P =
=
解析(I)从中任取1个球,求取得红球或黑球的概率,需要先算出此事件包含的基本事件数,以及所有的基本事件数,由公式求出即可;
(II)列出一次任取2个球的所有基本事件,由于小球只有颜色不同,故将红球编号为红1,红2,黑球编号为黑1,黑2,黑3,依次列举出所有的基本事件即可;
从中取2个球,求至少有一个红球的概率,从(II)知总的基本事件数有15种,至少有一个红球的事件包含的基本事件数有9种.由公式求出概率即可.
(III)从6只球中放回式的取两球一共有36种取法,其中至少有一个红球的取法共有20种,所以其中至少有一个红球概率为
解:(1)从6只球中任取1球得红球有2种取法,得黑球有3种取法,得红球或黑球的共有2+3=5种不同取法,任取一球有6种取法,所以任取1球得红球或黑球的概率得 .
.
(2)将红球编号为红1,红2,黑球编号为黑1,黑2,黑3,则一次任取2个球的所有基本事件为:
红1红2 红1黑1 红1黑2 红1黑3 红1白
红2白 红2黑1 红2黑2 红2黑3 黑1黑2
黑1黑3 黑1白 黑2黑3 黑2白 黑3白
从6只球中不放回的取两球一共有15种取法,其中至少有一个红球的取法共有9种,所以其中至少有一个红球概率为 。
。
(3)从6只球中放回式的取两球一共有36种取法,其中至少有一个红球的取法共有20种,所以其中至少有一个红球概率为P =
=

 天天练口算系列答案
天天练口算系列答案(本题14分)某校高二年级研究性学习小组,为了分析2011年我国宏观经济形势,上网查阅了2010年和2011年2-6月我国CPI同比(即当年某月与前一年同月相比)的增长数据(见下表),但2011年4,5,6三个月的数据(分别记为x,y,z)没有查到.有的同学清楚记得2011年2,3,4,5,6五个月的CPI数据成等差数列.
(1)求x,y,z的值;
(2)求2011年2-6月我国CPI的数据的方差;
(3)一般认为,某月CPI达到或超过3个百分点就已经通货膨胀,而达到或超过5个百分点则严重通货膨胀.现随机地从上表2010年的五个月和2011年的五个月的数据中各抽取一个数据,求相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率.
附表:我国2010年和2011年2~6月的CPI数据(单位:百分点.注:1个百分点=1%)
| 年份 | 二月 | 三月 | 四月 | 五月 | 六月 |
| 2010 | 2.7 | 2.4 | 2.8 | 3.1 | 2.9 |
| 2011 | 4.9 | 5.0 | x | y | z |
 个等级,等级系数
个等级,等级系数 依次为
依次为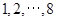 ,其中
,其中 为标准
为标准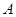 ,
,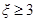 为标准
为标准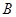 ,产品的等级系数越大表明产品的质量越好,已知某厂执行标准
,产品的等级系数越大表明产品的质量越好,已知某厂执行标准 件,相应的等级系数组成一个样本,数据如下:
件,相应的等级系数组成一个样本,数据如下: 的为一等品,等级系数
的为一等品,等级系数 的为二等品,等级系数
的为二等品,等级系数 的为三等品.
的为三等品.