题目内容
(本小题满分12分)甲、乙两人各进行一次射击,如果两人击中目标的概率都是0.6,计算:
(1)两人都击中目标的概率;
(2)其中恰有一人击中目标的概率;
(3)至少有一人击中目标的概率.
解:(1)我们把“甲射击一次击中目标”叫做事件A,“乙射击一次击中目标”叫做事件B.显然事件A、B相互独立,所以两人各射击一次都击中目标的概率是P(A·B)?=P(A)·P(B)=0.6×0.6 =0.36.
=0.36.
答:两人都击中目标的概率是0.36. …………………………………4分
(2)同理,两人各射击一次,甲击中、乙未击中的概率是P(A·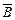 )=P(A)·P(
)=P(A)·P(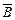 )
)
=0.6× (1-0.6)=0.6×0.4=0.24.
甲未击中、乙击中的概率是P(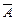 ·B)=P(
·B)=P(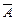 )P(B)=0.24,显然,“甲击中、乙未击中”和“甲未击中、乙击中”是不可能同时发生,即事件A·
)P(B)=0.24,显然,“甲击中、乙未击中”和“甲未击中、乙击中”是不可能同时发生,即事件A·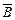 与
与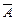 ·B互斥,所以恰有一人击中目标的概率是P(A·
·B互斥,所以恰有一人击中目标的概率是P(A·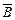 )+P(
)+P(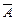 ·B)=0.24+0.24=0.48.
·B)=0.24+0.24=0.48.
答:其中恰有一人击中目标的概率是0.48. …………………………………8分
(3)两人各射击一次,至少有一人击中目标的概率P=P(A·B)+[P(A·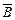 )+P(
)+P(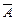 )·B]=0.
)·B]=0. 36+0.48=0.84
36+0.48=0.84
答:至少有一人击中目标的概率是0.84. ………………………………12分
解析

练习册系列答案
相关题目
某校教务处要对高三上学期期中数学试卷进行调研,考察试卷中某道填空题的得分情况.已知该题有两空,第一空答对得3分,答错或不答得0分;第二空答对得2分,答错或不答得0分.第一空答对与否与第二空答对与否是相互独立的.从该校1468份试卷中随机抽取1000份试卷,其中该题的得分组成容量为1000的样本,统计结果如下表:
| 第一空得分情况 | | 第二空得分情况 | ||||
| 得分 | 0 | 3 | | 得分 | 0 | 2 |
| 人数 | 198 | 802 | | 人数 | 698 | 302 |
(Ⅱ)该校的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题得分
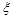 的数学期望.
的数学期望.  ,笔试考试成绩每次合格的概率均为
,笔试考试成绩每次合格的概率均为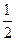 ,假设各次考试成绩合格与否均互不影响.
,假设各次考试成绩合格与否均互不影响.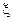 ,求参加考试次数
,求参加考试次数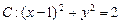 ,点
,点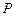 是圆内的任意一点,直线
是圆内的任意一点,直线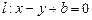 .
.  ;
;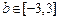 ,求直线
,求直线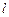 与
与 圆
圆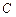 相交的概率.
相交的概率.