题目内容
（2012•虹口区二模）如果(x+
)n展开式中，第4项与第6项的系数相等，则该展开式中，常数项的值是
| 1 | x |
70
70
．分析：根据二项式定理，写出(x+
)n展开式的通项，可得其系数，结合题意，可得Cn3=Cn5，解可得n的值为8，令x的指数为0，可得r=4，将r=4代入通项，可以求出常数项，即可得答案．
| 1 |
| x |
解答：解：(x+
)n展开式的通项为Tr+1=Cnrxn-rxr=Cnrxn-2r，其系数为Cnr，
若第4项与第6项的系数相等，则有Cn3=Cn5，
则n=8，
则在其通项中，令8-2r=0，可得r=4，
则其常数项为第5项，有T5=C84=70，
故答案为70．
| 1 |
| x |
若第4项与第6项的系数相等，则有Cn3=Cn5，
则n=8，
则在其通项中，令8-2r=0，可得r=4，
则其常数项为第5项，有T5=C84=70，
故答案为70．
点评：本题考查二项式定理的应用，关键是正确写出二项式的展开式，结合题意，求出n的值．
练习册系列答案
相关题目
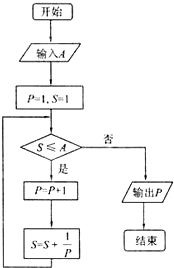（2012•虹口区二模）执行如图所示的程序框图，若输入A的值为2，则输出P的值为