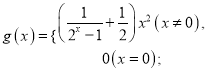题目内容
【题目】从某企业生产的某种产品中抽取500件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图：
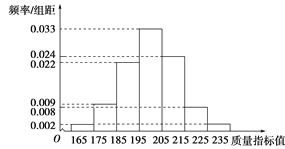
(1)求这500件产品质量指标值的样本平均数
和样本方差s2(同一组中的数据用该组区间的中点值作代表)；
(2)由直方图可以认为，这种产品的质量指标值Z服从正态分布N(μ，σ2)，其中μ近似为样本平均数
，σ2近似为样本方差s2.
(ⅰ)利用该正态分布，求P(187.8<Z<212.2)；
(ⅱ)某用户从该企业购买了100件这种产品，记X表示这100件产品中质量指标值位于区间(187.8，212.2)的产品件数.利用(ⅰ)的结果，求E(X).
附： 
≈12.2.若Z～N(μ，σ2)，则P(μ－σ<Z<μ＋σ)＝0.682 6，P(μ－2σ<Z<μ＋2σ)＝0.954 4.
【答案】（1）150（2）(ⅰ) 0.6826. (ⅱ) 68.26.
【解析】试题分析：
(1)利用题中所给的数据可得平均数
，方差
；
(2)利用正态分布的对称性可得：P(187.8<Z<212.2)＝0.6826.
(3)利用(i)的结论结合题意可得
.
试题解析：
(1)抽取产品的质量指标值的样本平均数x－和样本方差s2分别为
＝170×0.02＋180×0.09＋190×0.22＋200×0.33＋210×0.24＋220×0.08＋230×0.02＝200，
s2＝(－30)2×0.02＋(－20)2×0.09＋(－10)2×0.22＋0×0.33＋102×0.24＋202×0.08＋302×0.02＝150.
(2)(ⅰ)由(1)知，Z～N(200，150)，从而
P(187.8<Z<212.2)＝P(200－12.2<Z<200＋12.2)＝0.6826.
(ⅱ)由(ⅰ)知，一件产品的质量指标值位于区间(187.8，212.2)的概率为0.682 6，依题意知X～B(100，0.6826)，所以E(X)＝100×0.682 6＝68.26.
