题目内容
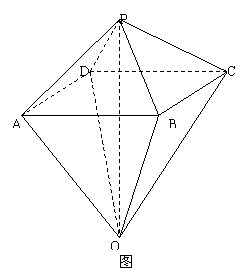
如图4, 已知两个正四棱锥![]() 的高分别为1和2,
的高分别为1和2, ![]()
(Ⅰ) 证明: ![]() ;
;
(Ⅱ) 求异面直线AQ与PB所成的角;
(Ⅲ) 求点![]() 到平面
到平面![]() 的距离.
的距离.

解析:解法一:(Ⅰ).连结AC、BD,设![]() .由P-ABCD与Q-ABCD
.由P-ABCD与Q-ABCD
都是正四棱锥,所以PO⊥平面ABCD,QO⊥平面ABCD.
从而P、O、Q三点在一条直线上,所以PQ⊥平面ABCD.
(II)由题设知,ABCD是正方形,所以![]() .由(I),
.由(I),![]() 平面
平面![]() ,故可以分别以直线CA、DB、QP为
,故可以分别以直线CA、DB、QP为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系(如图),
轴建立空间直角坐标系(如图),
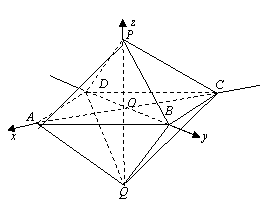
由题设条件,相关各点的坐标分别是![]() ,
,![]() ,
,![]()
所以![]() ,
,![]() ,于是
,于是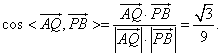
从而异面直线AQ与PB所成的角是![]() .
.
(Ⅲ).由(Ⅱ),点D的坐标是(0,-![]() ,0),
,0),![]() ,
,
![]() ,设
,设![]() 是平面QAD的一个法向量,
是平面QAD的一个法向量,
由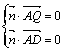 得
得![]() .
.
取x=1,得![]() . 所以点P到平面QAD的距离
. 所以点P到平面QAD的距离 .
.
解法二:(Ⅰ).取AD的中点M,连结PM,QM.因为P-ABCD与Q-ABCD
都是正四棱锥,所以AD⊥PM,AD⊥QM. 从而AD⊥平面PQM.
又![]() 平面PQM,所以PQ⊥AD.同理PQ⊥AB,所以PQ⊥平面ABCD.
平面PQM,所以PQ⊥AD.同理PQ⊥AB,所以PQ⊥平面ABCD.
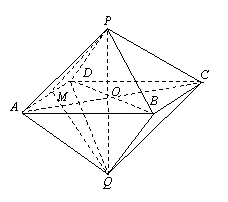
(Ⅱ).连结AC、BD设![]() ,由PQ⊥平面ABCD及正四棱锥的性质可知O在
,由PQ⊥平面ABCD及正四棱锥的性质可知O在
PQ上,从而P、A、Q、C四点共面.
取OC的中点N,连结PN.
因为![]() ,所以
,所以![]() ,
,
从而AQ∥PN.∠BPN(或其补角)是异面直线AQ
与PB所成的角.连接BN,
因为![]() .
.
![]()
![]()
所以![]() .
.
从而异面直线AQ与PB所成的角是![]() .
.
(Ⅲ).由(Ⅰ)知,AD⊥平面PQM,所以平面PQM⊥平面QAD. 过P作PH⊥QM
于H,则PH⊥平面QAD,所以PH的长为点P到平面QAD的距离.
连结OM,则![]() .所以
.所以![]() ,
,
又PQ=PO+QO=3,于是![]() .
.
即点P到平面QAD的距离是![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
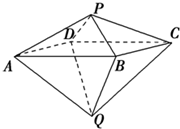 如图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.
如图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.
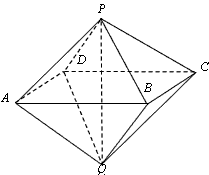
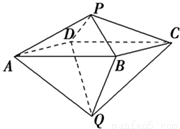 如图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.
如图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.