题目内容
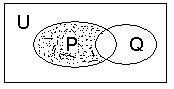
(08年龙岩一中模拟文)右图中阴影部分表示的集合是（ ）
A．
B． 
C．（） D．（
）
答案：A
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
(08年龙岩一中模拟文)右图中阴影部分表示的集合是（ ）
A． B．
C．（） D．（）
阅读快车系列答案
平面ABC，PC=AC=2，AB=BC，D是PB上一点，且CD
的一元二次方程
，求上述方程有两个不相等实根的概率．
，
．
时，
在
上是增函数；
，试说明存在实数 
，当
时，
．
的前n项和为
，已知
的通项公式；
记
并证明
.
分. 现从盒内一次性取3个球.
为取出的3个球中白色球的个数，求