题目内容
(08年龙岩一中模拟理)(14分)
已知函数![]() ,
,![]() .
.
(1)证明:当![]() 时,
时,![]() 在
在![]() 上是增函数;
上是增函数;
(2)对于给定的闭区间![]() ,试说明存在实数
,试说明存在实数 ![]() ,当
,当![]() 时,
时,![]() 在闭区间
在闭区间![]() 上是减函数;
上是减函数;
(3)证明:![]() .
.
解析:(1)证明:由题设得![]()
又由![]() ≥
≥![]() ,且t<
,且t<![]() 得t<
得t<![]() ,
,
即![]() >0
>0![]() 由此可知,
由此可知,![]() 为R上的增函数. 4分
为R上的增函数. 4分
(2)证法一:因为![]() <0是
<0是![]() 为减函数的充分条件,所以只要找到实数k,使得
为减函数的充分条件,所以只要找到实数k,使得
![]() <0,即t>
<0,即t>![]() 在闭区间[a,b]上成立即可.
在闭区间[a,b]上成立即可.
因此y=![]() 在闭区间[a,b]上连续,故在闭区[a,b]上有最大值,设其为k,t>k时,
在闭区间[a,b]上连续,故在闭区[a,b]上有最大值,设其为k,t>k时, ![]() <0在闭区间[a,b]上恒成立,即
<0在闭区间[a,b]上恒成立,即![]() 在闭区间[a,b]上为减函数. 8分
在闭区间[a,b]上为减函数. 8分
(3)证法一:设![]()
![]() 易得
易得![]() ≥
≥![]() .
.
令![]() 则
则![]() 易知
易知![]()
当x>0时, ![]() >0;当x<0,
>0;当x<0,![]() <0
<0![]() 故当x=0时,
故当x=0时,![]() 取最小值,
取最小值,![]() 所以
所以![]() ≥
≥![]() ,于是对任意x、t,有
,于是对任意x、t,有![]() ≥
≥![]() ,即
,即![]() ≥
≥![]() . 14分
. 14分
(2)证法二:因为![]() <0是
<0是![]() 为减函数的充分条件,所以只要找到实数k,使得t>k时
为减函数的充分条件,所以只要找到实数k,使得t>k时
![]() <0,在闭区间[a,b]上成立即可.
<0,在闭区间[a,b]上成立即可.
令![]() 则
则![]() <0(
<0(![]() )当且仅当
)当且仅当![]() <0(
<0(![]() ).
).
而上式成立只需
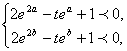 即
即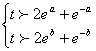
成立.取![]() 与
与![]() 中较大者记为k,易知当t>k时,
中较大者记为k,易知当t>k时,![]() <0在闭区[a,b]成立,即
<0在闭区[a,b]成立,即![]() 在闭区间[a,b]上为减函数.
在闭区间[a,b]上为减函数.
(3)证法二:设![]() =
=![]()
![]() ≥
≥![]() ,当且仅当
,当且仅当![]() ≥0
≥0
只需证明
![]() ≤0,即
≤0,即![]() ≥1
≥1
以下同证法一.
证法三:设![]() =
=![]() ,则
,则![]()
易得![]() 当t>
当t>![]() 时,
时, ![]() >0; t<
>0; t<![]() 时,
时, ![]() <0,故当t=
<0,故当t=![]()
![]() 取最小值
取最小值![]() 即
即![]() ≥
≥![]()
以下同证法一.证法四: ![]()
![]()
设点A、B的坐标分别为![]() ,易知点B在直线y=x上,令点A到直线y=离为d,则
,易知点B在直线y=x上,令点A到直线y=离为d,则![]()
![]() ≥
≥![]() 以下同证法一.
以下同证法一.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
