题目内容
(本小题共13分)
在平面直角坐标系 中,已知圆
中,已知圆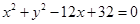 的圆心为
的圆心为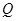 ,过点
,过点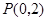 且斜率为
且斜率为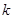 的直线
的直线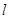 与圆
与圆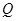 相交于不同的两点
相交于不同的两点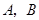 .
.
(Ⅰ)求圆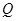 的面积;
的面积;
(Ⅱ)求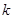 的取值范围;
的取值范围;
(Ⅲ)是否存在常数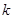 ,使得向量
,使得向量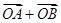 与
与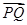 共线?如果存在,求
共线?如果存在,求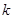 的值;如果不存在,请说
的值;如果不存在,请说
明理由.
【答案】
(1)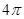 .
.
(2)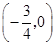
(3)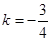
【解析】解:(Ⅰ)圆的方程可化为 ,可得圆心为
,可得圆心为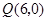 ,半径为2,
,半径为2,
故圆的面积为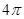 .
---------------------3分
.
---------------------3分
(Ⅱ)设直线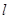 的方程为
的方程为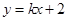 .
.
法一:
将直线方程代入圆方程得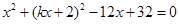 ,
,
整理得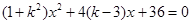 . ① ---------------------4分
. ① ---------------------4分
直线与圆交于两个不同的点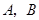 等价于
等价于
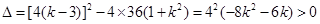 , ---------------------6分
, ---------------------6分
解得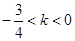 ,即
,即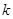 的取值范围为
的取值范围为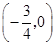 . ---------------------8分
. ---------------------8分
法二:
直线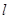 与圆
与圆 交于两个不同的点
交于两个不同的点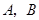 等价于
等价于
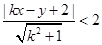 ---------------------5分
---------------------5分
化简得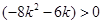 ,
,
解得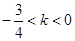 ,即
,即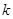 的取值范围为
的取值范围为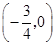 . ---------------------8分
. ---------------------8分
(Ⅲ)设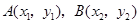 ,则
,则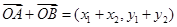 ,由方程①,
,由方程①,
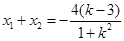 ②
②
又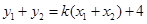 .
③
---------------------10分而
.
③
---------------------10分而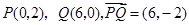 .
.
所以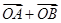 与
与 共线等价于
共线等价于 ---------------------11分
---------------------11分
将②③代入上式,解得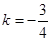 . ---------------------12分
. ---------------------12分

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 .
. 在
在 处取得极值,求a的值;
处取得极值,求a的值; 在
在 上的最大值.
上的最大值. ,设函数
,设函数 .
. 在
在 上的单调递增区间;
上的单调递增区间; 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,
的对边, ,
, ,
, ,求边
,求边 ,求
,求
 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式; 的条件下,求
的条件下,求 的值.
的值.