题目内容

设圆的切线与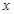轴的正半轴、轴的正半轴分别交于点，当取最小值时，切线的方程为________________。

 

【答案】

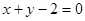
【解析】因为根据圆的切线与x轴，y轴交点分别为A和B，设出两点的坐标，进而得出切线的截距式方程，且根据勾股定理表示出|AB|，由直线与圆相切，得到圆心到直线的距离等于圆的半径，利用点到直线的距离公式表示出圆心到所设切线的距离d，使d等于圆的半径r，化简可得a与b的关系式，利用此关系式把|AB|2进行变形，利用基本不等式求出|AB|2的最小值，且得到取最小值时a与b的值，把此时a与b的值代入所设的方程中，即可确定出切线的方程x+y-2=0.

 

练习册系列答案
相关题目
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．请在答题纸指定区域内 作答．解答应写出文字说明、证明过程或演算步骤．
A．如图，圆O的直径AB=6，C为圆周上一点，BC=3，过C作圆的切线l，过A作l的垂线AD，AD分别与直线l、圆交于点D、E．求∠DAC的度数与线段AE的长．
B．已知二阶矩阵A=
2a
b0
属于特征值-1的一个特征向量为
1
-3
，求矩阵A的逆矩阵．

C．已知极坐标系的极点在直角坐标系的原点，极轴与x轴的正半轴重合，曲线C的极坐标方程ρ2cos2θ+3ρ2sin2θ=3，直线l的参数方程为
x=-
3
t
y=1+t
（t为参数，t∈{R}）．试求曲线C上点M到直线l的距离的最大值．
D．（1）设x是正数，求证：（1+x）（1+x2）（1+x3）≥8x3；
（2）若x∈R，不等式（1+x）（1+x2）（1+x3）≥8x3是否仍然成立？如果仍成立，请给出证明；如果不成立，请举出一个使它不成立的x的值．
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分，请在答题纸指定区域内作答，解答应写出文字说明、证明过程或演算步骤．
A．选修4-1：（几何证明选讲）
如图，从O外一点P作圆O的两条切线，切点分别为A，B，
AB与OP交于点M，设CD为过点M且不过圆心O的一条弦，
求证：O，C，P，D四点共圆．
B．选修4-2：（矩阵与变换）
已知二阶矩阵M有特征值λ=3及对应的一个特征向量e1=[
 
1
1
]，并且矩阵M对应的变换将点（-1，2）变换成（9，15），求矩阵M．
C．选修4-4：（坐标系与参数方程）
在极坐标系中，曲线C的极坐标方程为p=2
2
sin（θ-
π
4
），以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
x=1+
4
5
t
y=-1-
3
5
t
（t为参数），求直线l被曲线C所截得的弦长．
D．选修4-5（不等式选讲）
已知实数x，y，z满足x+y+z=2，求2x2+3y2+z2的最小值．
（选做题）在A，B，C，D四小题中只能选做2题，每小题10分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．
A．选修4-1：几何证明选讲
如图，⊙O的半径OB垂直于直径AC，M为AO上一点，BM的延长线交⊙O于N，过
N点的切线交CA的延长线于P．
（1）求证：PM2=PA•PC；
（2）若⊙O的半径为2
3
，OA=
3
OM，求MN的长．
B．选修4-2：矩阵与变换
曲线x2+4xy+2y2=1在二阶矩阵M=
.
1a
b1
.
的作用下变换为曲线x2-2y2=1，求实数a，b的值；
C．选修4-4：坐标系与参数方程
在极坐标系中，圆C的极坐标方程为ρ=
2
cos(θ+
π
4
)，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
x=1+
4
5
t 
y=-1-
3
5
t 
（t为参数），求直线l被圆C所截得的弦长．
D．选修4-5：不等式选讲
设a，b，c均为正实数．
（1）若a+b+c=1，求a2+b2+c2的最小值；
（2）求证：
1
2a
+
1
2b
+
1
2c
≥
1
b+c
+
1
c+a
+
1
a+b
．
[选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．
A．（选修4-1：几何证明选讲）
如图，圆O的直径AB=8，C为圆周上一点，BC=4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，求线段AE的长．
B．（选修4-2：矩阵与变换）
已知二阶矩阵A有特征值λ1=3及其对应的一个特征向量α1=
1
1
，特征值λ2=-1及其对应的一个特征向量α2=
1
-1
，求矩阵A的逆矩阵A-1．
C．（选修4-4：坐标系与参数方程）
以平面直角坐标系的原点O为极点，x轴的正半轴为极轴，建立极坐标系（两种坐标系中取相同的单位长度），已知点A的直角坐标为（-2，6），点B的极坐标为(4，
π
2
)，直线l过点A且倾斜角为
π
4
，圆C以点B为圆心，4为半径，试求直线l的参数方程和圆C的极坐标方程．
D．（选修4-5：不等式选讲）
设a，b，c，d都是正数，且x=
a2+b2
，y=
c2+d2
．求证：xy≥
(ac+bd)(ad+bc)
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网