题目内容
函数f(x)=xlnx,g(x)=x3+ax2-x+2
(1)如果函数g(x)单调减区调为 ,求函数g(x)解析式;
,求函数g(x)解析式;
(2)在(1)的条件下,求函数y=g(x)图象过点p(1,1)的切线方程;
(3)若 x0∈(0,+∞),使关于x的不等式2f(x)≥g'(x)+2成立,求实数a取值范围.
x0∈(0,+∞),使关于x的不等式2f(x)≥g'(x)+2成立,求实数a取值范围.
(1)如果函数g(x)单调减区调为
 ,求函数g(x)解析式;
,求函数g(x)解析式;(2)在(1)的条件下,求函数y=g(x)图象过点p(1,1)的切线方程;
(3)若
 x0∈(0,+∞),使关于x的不等式2f(x)≥g'(x)+2成立,求实数a取值范围.
x0∈(0,+∞),使关于x的不等式2f(x)≥g'(x)+2成立,求实数a取值范围.解:(1)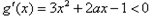 解为
解为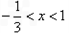
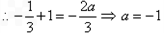
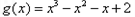
(2)设切点为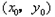 ,则切线方程为
,则切线方程为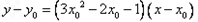
(1,1)代入得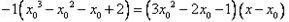
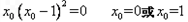
切线方程为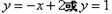
(3)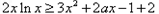
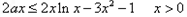 有解
有解
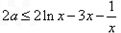 最大值
最大值
令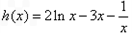 ,则
,则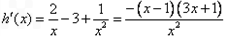
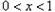 时
时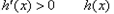 单增,
单增,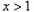 时
时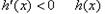 单减
单减
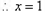 时,
时,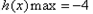

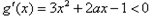 解为
解为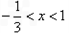
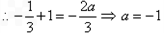
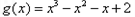
(2)设切点为
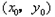 ,则切线方程为
,则切线方程为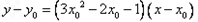
(1,1)代入得
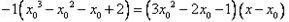
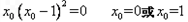
切线方程为
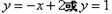
(3)
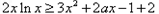
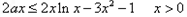 有解
有解 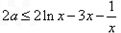 最大值
最大值 令
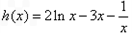 ,则
,则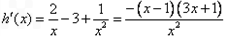
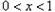 时
时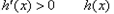 单增,
单增,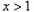 时
时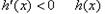 单减
单减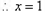 时,
时,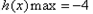


练习册系列答案
相关题目
 (其中e=2.71828…是自然对数的底数);
(其中e=2.71828…是自然对数的底数);
 )
)