题目内容
(2007
成都模拟)已知函数f(x)=xln x.(1)
求函数f(x)的单调区间和最小值;(2)
当b>0时,求证: (其中e=2.71828…是自然对数的底数);
(其中e=2.71828…是自然对数的底数);
(3)若a>0,b>0,证明:f(a)+(a+b)ln2≥f(a+b)-f(b).
答案:略
解析:
解析:
|
解析: (1)∵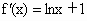 (x>0),令 (x>0),令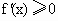 ,即 ,即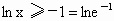 . .
∵ e=2.71828…>1,∴y=lnx在区间(0,+∞)上是单调递增函数.∴ 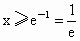 .∴ .∴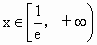 .同理,令 .同理,令 可得 可得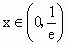 . .
∴ f(x)的单调递增区间为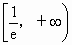 ,f(x)的单调递减区间为 ,f(x)的单调递减区间为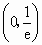 . .
由此可知 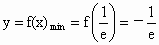 . .
(2) 由(1)可知当b>0时,有 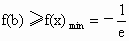 ,∴ ,∴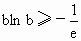 , ,
即 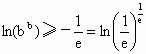 . .
∴ 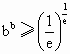 . .
(3) 将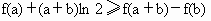 变形,得 变形,得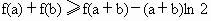 , ,
即证 设函数 g(x)=f(x)+f(k-x)(k>0).∵ f(x)=xlnx,∴ g(x)=xlnx+(k-x)ln(k-x),∴ 0<x<k.∵  ,令 ,令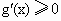 , ,
则有 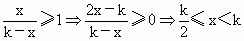 . .
∴函数 g(x)在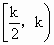 上单调递增,在 上单调递增,在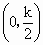 上单调递减. 上单调递减.
∴函数 g(x)的最小值为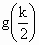 ,即总有 ,即总有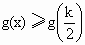 . .
而 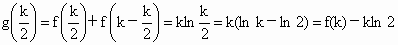 , ,
∴ 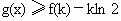 , ,
即 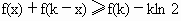 . .
令 x=a,k-x=b,则k=a+b.∴  . .
∴ 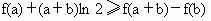 . . |

练习册系列答案
相关题目
(2007
成都模拟)已知无穷等比数列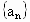 的公比为
的公比为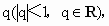
 为其前n项和
为其前n项和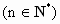 ,又
,又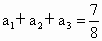 ,
,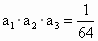 ,则
,则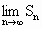 的值为
的值为
[
]|
A .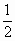 |
B .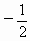 |
C .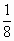 |
D .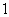 |
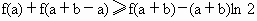
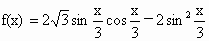 .
.
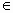 [0,π],求函数f(x)的值域;
[0,π],求函数f(x)的值域;
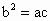 ,求sinA的值.
,求sinA的值.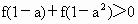 ,则实数a的取值范围为__________.
,则实数a的取值范围为__________.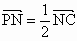 ,PM=MD.
,PM=MD.