题目内容
【题目】如下图所示的几何体中， 
为三棱柱，且
，四边形
为平行四边形， 
， 
.
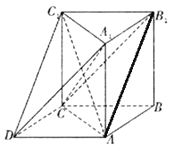
（1）求证： 
；
（2）若
，求证： 
；
（3）若
，二面角
的余弦值为若
，求三棱锥
的体积．
【答案】（1）详见解析；（2）详见解析；（3）4.
【解析】试题分析： 
连
交
于
点， 
为
的中点， 
为
的中点，
即
为
的中位线，即可依据线面平行的判定定理证得
根据线面垂直的判定定理要证一条直线不两条相交直线垂直，可得
，结合余弦定理得
.
（3）先做出二面角的平面角，解得长度，再根据等体积法求得结果。
解析：（1）连
交
于
点，连
交
于
点，则
.
由平几知： 
为
的中点， 
为
的中点，
即
为
的中位线. 
.
又
.
（2）
.
又
.
在
中由余弦定理知： 
.
又
.
又
.
又
.
（3）作
交
于
，连
，由（2）知： 
.
.
；由
知： 
得
；
在
中由平几知： 
，于是得
为正方形.
由（2）知： 
.
练习册系列答案
阅读快车系列答案
相关题目
【题目】某种零件按质量标准分为1，2，3，4，5五个等级，现从一批该零件巾随机抽取20个，对其等级进行统计分析，得到频率分布表如下
等级 | 1 | 2 | 3 | 4 | 5 |
频率 | 0.05 | m | 0.15 | 0.35 | n |
（1）在抽取的20个零件中，等级为5的恰有2个，求m，n；
（2）在（1）的条件下，从等级为3和5的所有零件中，任意抽取2个，求抽取的2个零件等级恰好相同的概率．
